圆形练习题及答案(三)
概要:此,∵两圆外切,圆心距为5cm,若一个圆的半径是3cm,∴另一个圆的半径=5﹣3=2(cm)。故选D。2.(2012四川乐山)⊙1的半径为3厘米,⊙2的半径为2厘米,圆心距⊙1⊙2=5厘米,这两圆的位置关系是()A.内含B.内切C.相交D.外切【答案】D。【考点】两圆的位置关系。【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,∵⊙O1的半径r=3,⊙O2的半径r=2,∴3+2=5。∵两圆的圆心距为O1O2=5,∴两圆的位置关系是外切。故选D。3.(2012四川内江)如图,AB是⊙的直径,弦CD⊥A,∠CDB=300,CD=,则阴影部分图形的面积为() A.B.C.D.【答案】D。【考点】垂径定理,圆周角定理,锐角三角函数定义,特殊角的三角函数值,扇形面积公式。【分析】连接OD。∵CD⊥AB,CD=,∴CE=DE=(垂径定理)。∴。∴阴影部分
圆形练习题及答案(三),http://www.jdxx5.com四川各市中考数学试题分类解析汇编专题11:圆
1、选择题
1.(2012四川成都3分)已知两圆外切,圆心距为5cm,若其中一个圆的半径是3cm,则另一个圆的半径是( )
A.8cm B.5cm C.3cm D.2cm
【答案】D。
【考点】两圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,∵两圆外切,圆心距为5cm,若一个圆的半径是3cm,∴另一个圆的半径=5﹣3=2(cm)。故选D。
2.(2012四川乐山)⊙1的半径为3厘米,⊙2的半径为2厘米,圆心距⊙1⊙2=5厘米,这两圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
【答案】D。
【考点】两圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,∵⊙O1的半径r=3,⊙O2的半径r=2,∴3+2=5。
∵两圆的圆心距为O1O2=5,∴两圆的位置关系是外切。故选D。
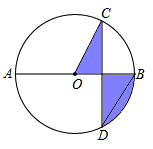
3.(2012四川内江)如图,AB是⊙的直径,弦CD⊥A,∠CDB=300,CD=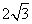 ,则阴影部分图形的面积为( )
,则阴影部分图形的面积为( )
A.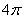 B.
B.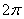 C.
C.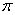 D.
D.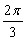
【答案】D。
【考点】垂径定理,圆周角定理,锐角三角函数定义,特殊角的三角函数值,扇形面积公式。
【分析】连接OD。
∵CD⊥AB,CD=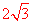 ,∴CE=DE=
,∴CE=DE=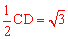 (垂径定理)。
(垂径定理)。
∴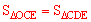 。∴阴影部分的面积等于扇形OBD的面积。
。∴阴影部分的面积等于扇形OBD的面积。
又∵∠CDB=30°,∠COB=∠BOD,∴∠BOD=60°(圆周角定理)。
∴OC=2。
∴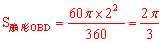 ,即阴影部分的面积为
,即阴影部分的面积为 。故选D。
。故选D。
4.(2012四川达州3分)如图,⊙O是△ABC的外接圆,连结OB、OC,若OB=BC,则∠BAC等于( )
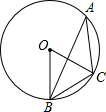
A、60° B、45° C、30° D、20°
【答案】C。
【考点】圆周角定理,等边三角形的判定和性质。
【分析】∵OB=BC=OC,∴△OBC是等边三角形。∴∠BOC=60°。
∴根据同弧所对圆周角是圆心角一半的性质,得∠BAC=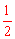 ∠BOC=30°。故选C。
∠BOC=30°。故选C。
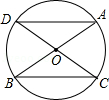
5.(2012四川德阳3分)已知AB、CD是⊙O的两条直径,∠ABC=30°,那么∠BAD=( )
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页

- 圆形练习题及答案(三)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
