圆形练习题及答案（三）

概要：．【答案】12。【考点】相切两圆的性质，矩形的判定和性质，含30度角的直角三角形的性质，勾股定理；；切线长定理。【分析】∵⊙O2的面积为π，∴⊙O2的半径是1。∵AB和AH是⊙O1的切线，∴AB=AH。设⊙O2的半径是R，连接DO2，DO1，O2E，O1H，AO1，作O2F⊥BC于F。∵⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线DC、DA，∠ADC=60°∴D．O2、O1三点共线，∠CDO1=30°。∴∠DAO1=60°，∠O2EC=∠ECF=∠CFO2=90°。∴四边形CFO2E是矩形，∴O2E=CF，CE=FO2，∠FO2O1=∠CDO1=30°。∴DO2=2O2E=2，∠HAO1=60°，R+1=2（R﹣1），解得：R=3。即DO1=2+1+3=6，在Rt△CDO1中，由勾股定理得：CD=。∵∠HO1A=90°﹣60°=30°，HO1=3，∴AH==AB。&th

∵高线长为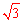，底面的半径是1，∴由勾股定理知：母线长=。

∴圆锥侧面积=×底面周长×母线长=×2π×2=2π。

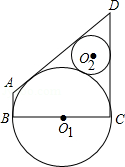
5.（2012四川攀枝花4分）如图，以BC为直径的⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线交于点D，且∠ADC=60°，过B点的⊙O1的切线交其中一条外公切线于点A．若⊙O2的面积为π，则四边形ABCD的面积是▲．

【答案】12。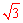

【考点】相切两圆的性质，矩形的判定和性质，含30度角的直角三角形的性质，勾股定理；；切线长定理。

【分析】∵⊙O2的面积为π，∴⊙O2的半径是1。

∵AB和AH是⊙O1的切线，∴AB=AH。

设⊙O2的半径是R，连接DO2，DO1，O2E，O1H，AO1，作O2F⊥BC于F。

∵⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线DC、DA，∠ADC=60°

∴D．O2、O1三点共线，∠CDO1=30°。

∴∠DAO1=60°，∠O2EC=∠ECF=∠CFO2=90°。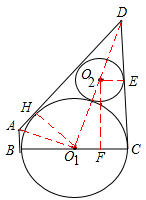

∴四边形CFO2E是矩形，

∴O2E=CF，CE=FO2，∠FO2O1=∠CDO1=30°。

∴DO2=2O2E=2，∠HAO1=60°，R+1=2（R﹣1），解得：R=3。

即DO1=2+1+3=6，

在Rt△CDO1中，由勾股定理得：CD=。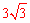

∵∠HO1A=90°﹣60°=30°，HO1=3，∴AH=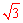=AB。

∴四边形ABCD的面积是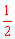：×（AB+CD）×BC=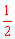×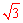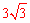（+）×（3+3）=12。

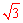6.（2012四川宜宾3分）如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是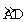的中点，弦CE⊥AB于点F，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：

①∠BAD=∠ABC；②GP=GD；③点P是△ACQ的外心；④AP•AD=CQ•CB．

其中正确的是▲（写出所有正确结论的序号）．

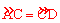
【答案】②③④。

【考点】切线的性质，圆周角定理，三角形的外接圆与外心，等腰三角形的判定和性质，相似三角形的判定和性质。

【分析】①如图，连接BD，

∵点C是的中点，∴∠ABC =∠CBD，即∠ABD=2∠ABC。

又∵AB为圆O的直径，∴∠ADB=90°。

∴∠BAD＋∠ABD=900，即∠BAD＋2∠ABC =900。

∴当∠ABC =300时，∠BAD=∠ABC；当∠ABC ≠300时，∠BAD≠∠ABC。

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页