圆形练习题及答案（三）

概要：可能【答案】B。【考点】坐标与图形性质，直线与圆的位置关系，等腰直角三角形的判定和性质，勾股定理。【分析】如图，在中，令x=0，则y=－；令y=0，则x=，∴A（0，－），B（，0）。∴OA=OB= 2 。∴△AOB是等腰直角三角形。∴AB=2，过点O作OD⊥AB，则OD=BD=AB=×2=1。又∵⊙O的半径为1，∴圆心到直线的距离等于半径。∴直线y=x- 2 与⊙O相切。故选B。7.（2012四川巴中3分）已知两圆的半径分别为1和3，当这两圆内含时，圆心距d的范围是（）A. 0B.0≤d＜3C.0≤d＜2D.0≤d＜3－1【答案】D。【考点】圆与圆的位置关系。【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。因此，由题意知，两圆内含，则0≤d＜3－1。故选D。8.（2012四川自贡3分）如图，圆锥形冰淇淋盒的母线长是13cm，高

A.45°　　　B. 60°　　　C.90°　　D. 30°

【答案】D。

【考点】圆周角定理，等腰三角形的性质。

【分析】∵∠ADC与∠ABC所对的弧相同，∴∠ADC=∠ABC=30°。

∵OA=OD，∴∠BAD =∠ADC 30°，故选D。

6.（2012四川凉山）如图，在平面直角坐标系中，⊙O的半径为1，则直线与⊙的位置关系是（　）　

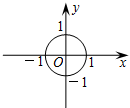
A．相离　　　　　　B．相切　　　　　　C．相交　　　　D．以上三种情况都有可能

【答案】B。

【考点】坐标与图形性质，直线与圆的位置关系，等腰直角三角形的判定和性质，勾股定理。

【分析】如图，在中，令x=0，则y=－；令y=0，则x=，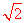

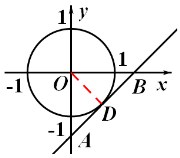∴A（0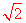，－），B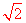（，0）。∴OA=OB= 2 。

∴△AOB是等腰直角三角形。∴AB=2，

过点O作OD⊥AB，则OD=BD=AB=×2=1。

又∵⊙O的半径为1，∴圆心到直线的距离等于半径。

∴直线y=x- 2 与⊙O相切。故选B。

7.（2012四川巴中3分）已知两圆的半径分别为1和3，当这两圆内含时，圆心距d的范围是（　　）

【答案】D。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。因此，

由题意知，两圆内含，则0≤d＜3－1。故选D。

8.（2012四川自贡3分）如图，圆锥形冰淇淋盒的母线长是13cm，高是12cm，则该圆锥形底面圆的面积是（　　）

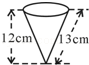A．10πcm2　　B．25πcm2　　C．60πcm2　　　D．65πcm2

【答案】B。

【考点】圆锥的计算，勾股定理。菁优网版权所有

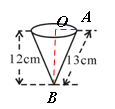
【分析】如图，在Rt△AOB中，圆锥的母线长AB=13cm，圆锥的OB=高12cm，

∴圆锥的底面半径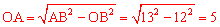（cm），

∴S =π×52=25π（cm2）。故选B。

9.（2012四川泸州2分）如图，在△ABC中，AB为⊙O的直径，∠B = 60°，∠BOD = 100°，则∠C的

度数为（　　）

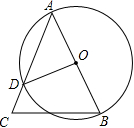A、50°　　　B、60°　　　C、70°　　D、80°

【答案】C。

【考点】圆周角定理，三角形的内角和定理。

【分析】∵∠BOD＝100°，∴∠A＝∠BOD＝50°。

∵∠B＝60°，∴∠C=180°－∠A－∠B=70°。故选C。

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页