圆形练习题及答案（三）
[10-09 23:31:05] 来源：http://www.jdxx5.com 初三数学试题 阅读：92676次
概要：。∴。∴∠ACP=∠CAP。∴PA=PC。∵AB是直径．∴∠ACB=90°。∴∠PCQ=90°－∠ACP，∠CQP=90°－∠CAP。∴∠PCQ=∠CQP。∴PC=PQ。∴PA=PQ，即P是AQ的中点。（2）∵，∴∠CAQ=∠ABC。又∵∠ACQ=∠BCQ，∴△CAQ∽△CBA。∴。又∵AQ=，BA=10，∴。设AC=3k，BC=4k，则由勾股定理得，，解得k=2。∴AC=6，BC=8。根据直角三角形的面积公式，得：AC•BC=AB•CH，∴6×8=10CH。∴CH=。又∵CH=HE，∴CE=2CH=。上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]
圆形练习题及答案（三）,http://www.jdxx5.com。∴
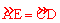。∴∠ACP=∠CAP。∴PA=PC。
∵AB是直径．∴∠ACB=90°。
∴∠PCQ=90°－∠ACP，∠CQP=90°－∠CAP。∴∠PCQ=∠CQP。∴PC=PQ。
∴PA=PQ，即P是AQ的中点。
（2）∵
，∴∠CAQ=∠ABC。
又∵∠ACQ=∠BCQ，∴△CAQ∽△CBA。∴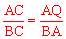
。
又∵AQ=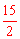
，BA=10，∴
。
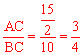设AC=3k，BC=4k，则由勾股定理得，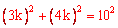
，解得k=2。
∴AC=6，BC=8。
根据直角三角形的面积公式，得：AC•BC=AB•CH，∴6×8=10CH。∴CH=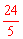
。
又∵CH=HE，∴CE=2CH=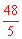
。
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]
标签:初三数学试题，九年级数学试题,初中数学学习方法，初中学习 - 初三学习 - 初三数学 - 初三数学试题
上一篇：圆形练习题及答案（四）
- 圆形练习题及答案（三）
- › 圆形练习题及答案汇总
- › 圆形练习题及答案（十）
- › 圆形练习题及答案（一）
- › 圆形练习题及答案（二）
- › 圆形练习题及答案（三）
- › 圆形练习题及答案（四）
- › 圆形练习题及答案（五）
- › 圆形练习题及答案（六）
- › 圆形练习题及答案（七）
- › 圆形练习题及答案（八）
- › 圆形练习题及答案（九）
最新《初三数学试题》
热门《初三数学试题》