圆形练习题及答案（三）

概要：D，故，从而可得出BD=DE，故BD=DE=DC，所以∠DEC=∠DCE，△ABC中由等腰三角形的性质可得出∠ABC=75°，故∠DEC=75°由三角形内角和定理得出∠EDC的度数，再根据BP∥DE可知∠PBC=∠EDC=30°，进而得出∠ABP的度数，再由OB=OP，可知∠OBP=∠OPB，由三角形内角和定理即可得出∠BOP=90°。（3）设OP交AC于点G，由∠BOP=90°可知∠AOG=90°在Rt△AOG中，由∠OAG=30°，可知，由得，，由∠AGO=∠CGP可得出△AOG∽△CPG，由相似三角形形的性质可知∠GPC=∠AOG=90°，故可得出CP是⊙O的切线。12.（2012四川自贡12分）如图AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．（1）若AB=2，∠P=30°，求AP的长；（2）若D为AP的中点，求证：直线CD是⊙O的切线．【答案】解：（1）∵AB是⊙O的直径，AP是⊙O的切线，&t

又∵∠AGO=∠CGP，∴△AOG∽△CPG。

∴∠GPC=∠AOG=90°。∴CP是⊙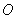的切线。

【考点】圆周角定理，等腰三角形的性质，三角形内角和定理，相似三角形的判定和性质，切线的判定。

【分析】（1）连接AD，由圆周角定理可知∠ADB=90°，再由AB=AC可知△ABC是等腰三角形，故BD=DC。

（2）由于AD是等腰三角形ABC底边上的中线，所以∠BAD=∠CAD，故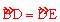，从而可得出BD=DE，故BD=DE=DC，所以∠DEC=∠DCE，△ABC中由等腰三角形的性质可得出∠ABC=75°，故∠DEC=75°由三角形内角和定理得出∠EDC的度数，再根据BP∥DE可知∠PBC=∠EDC=30°，进而得出∠ABP的度数，再由OB=OP，可知∠OBP=∠OPB，由三角形内角和定理即可得出∠BOP=90°。

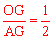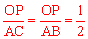（3）设OP交AC于点G，由∠BOP=90°可知∠AOG=90°在Rt△AOG中，由∠OAG=30°，可知，由得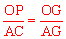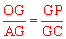，，由∠AGO=∠CGP可得出△AOG∽△CPG，由相似三角形形的性质可知∠GPC=∠AOG=90°，故可得出CP是⊙O的切线。

12.（2012四川自贡12分）如图AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．

（1）若AB=2，∠P=30°，求AP的长；

（2）若D为AP的中点，求证：直线CD是⊙O的切线．

【答案】解：（1）∵AB是⊙O的直径，AP是⊙O的切线，∴AB⊥AP。∴∠BAP=90°。

又∵AB=2，∠P=30°，∴AP=。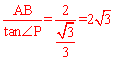

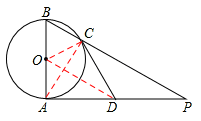（2）证明：如图，连接OC，OD．AC．

∵AB是⊙O的直径，

∴∠ACB=90°（直径所对的圆周角是直角）。

∴∠ACP=90°。

又∵D为AP的中点，∴AD=CD（直角三角形斜边上的中线等于斜边的一半）。

在△OAD和△OCD中，∵OA=OC，OD=DD，AD=CD，∴△OAD≌△OCD（SSS）。

∴∠OAD=∠OCD（全等三角形的对应角相等）。

又∵AP是⊙O的切线，A是切点，∴AB⊥AP。∴∠OAD=90°。

∴∠OCD=90°，即直线CD是⊙O的切线。

【考点】切线的判定和性质，锐角三角函数定义，特殊角的三角函数值，圆周角定理，直角三角形斜边上中线的性质，全等三角形的判定和性质。

【分析】（1）首先根据切线的性质判定∠BAP=90°；然后在Rt△ABP中利用三角函数的定义求得AP的长度。

（2）连接OC，OD、AC构建全等三角形△OAD≌△OCD，然后利用全等三角形的对应角相等推知∠OAD=∠OCD=90°，即OC⊥CD。

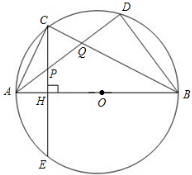
13.（2012四川泸州9分）如图，△ABC内接于⊙O，AB是⊙O的直径，C是的弧AD中点，弦CE⊥AB

于点H，连结AD，分别交CE、BC于点P、Q，连结BD。

(1)求证：P是线段AQ的中点；

(2)若⊙O的半径为5，AQ=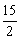，求弦CE的长。

【答案】解：（1）证明：∵AB是⊙O的直径，弦CE⊥AB，∴。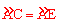

又∵C是弧的中点，∴

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页