圆形练习题及答案（三）

概要：⊙O的弦，OC⊥AB于C．若AB=，0C=1，则半径OB的长为▲．【答案】2。【考点】垂径定理，勾股定理。【分析】∵AB是⊙O的弦，OC⊥AB于C，AB=，∴BC=AB=。∵OC=1，∴在Rt△OBC中，。2.（2012四川成都4分）一个几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为▲ (结果保留π)【答案】68π。【考点】圆锥和圆柱的计算，勾股定理。【分析】圆锥的母线长是：。∴圆锥的侧面积是：×8π×5=20π，圆柱的侧面积是：8π×4=32π．几何体的下底面面积是：π×42=16π。∴该几何体的全面积（即表面积）为：20π+32π+16π=68π。3.（2012四川乐山3分）如图，⊙O是四边形ABCD的内切圆，E、F、G、H是切点，点P是优弧上异于E、H的点．若∠A=50°，则∠EPH=▲ ．【答案】65°。【考点】切线的性质，圆周角定理。【分析】如图，连接OE，OH，∵⊙O是四边形ABCD

10.（2012四川南充3分）一个圆锥的侧面积是底面积的2倍。则圆锥侧面展开图的扇形的圆心角是（　　）　

A .1200　　　B.1800　　　C.2400　　　D.3000

【答案】B。

【考点】圆锥的计算，扇形的弧长。

【分析】设母线长为R，底面半径为r，

∴底面周长=2πr，底面面积=πr2，侧面面积=πrR.

∵侧面积是底面积的2倍，∴R=2r。

设圆心角为n，有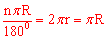，∴n=180°。故选B。

二、填空题

1.（2012四川成都4分）如图，AB是⊙O的弦，OC⊥AB于C．若AB=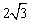，0C=1，则半径OB的长为▲　　．

【答案】2。

【考点】垂径定理，勾股定理。

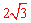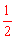【分析】∵AB是⊙O的弦，OC⊥AB于C，AB=，∴BC=AB=。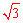

∵OC=1，∴在Rt△OBC中，。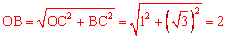

2.（2012四川成都4分）一个几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为　　▲　　 (结果保留π)

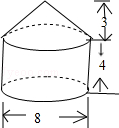
【答案】68π。

【考点】圆锥和圆柱的计算，勾股定理。

【分析】圆锥的母线长是：。

∴圆锥的侧面积是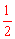：×8π×5=20π，

圆柱的侧面积是：8π×4=32π．

几何体的下底面面积是：π×42=16π。

∴该几何体的全面积（即表面积）为：20π+32π+16π=68π。

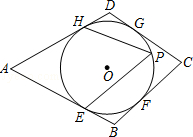
3.（2012四川乐山3分）如图，⊙O是四边形ABCD的内切圆，E、F、G、H是切点，点P是优弧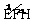上异于E、H的点．若∠A=50°，则∠EPH=　▲ 　．

【答案】65°。

【考点】切线的性质，圆周角定理。

【分析】如图，连接OE，OH，

∵⊙O是四边形ABCD的内切圆，E、F、G、H是切点，

∴∠OEA=∠OHA=90°。

又∵∠A=50°，

∴∠EOH=360°﹣∠OEA﹣∠OHA﹣∠A=360°﹣90°﹣90°﹣50°=130°。

又∵∠EPH和∠EOH分别是所对的圆周角和圆心角，

∴∠EP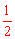H=∠EOH=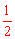×130°=65°。

4.（2012四川攀枝花4分）底面半径为1，高为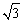的圆锥的侧面积等于▲　．

【答案】2π。

【考点】圆锥的计算，勾股定理。

【分析】由于高线，底面的半径，母线正好组成直角三角形，故母线长可由勾股定理求得，再由圆锥侧面积=

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页