圆形练习题及答案（三）

概要：点P在AB的延长线上，且∠CAB=2∠BCP．（1）求证：直线CP是⊙O的切线．（2）若BC=2，sin∠BCP=，求点B到AC的距离．（3）在第（2）的条件下，求△ACP的周长．【答案】解：（1）∵∠ABC=∠ACB且∠CAB=2∠BCP，在△ABC中，∠ABC+∠BAC+∠BCA=180°，∴2∠BCP+2∠BCA=180°。∴∠BCP+∠BCA=90°，即∠PCA=90°。又∵AC是⊙O的直径，∴直线CP是⊙O的切线。（2）如图，作BD⊥AC于点D，∵PC⊥AC，∴BD∥PC。∴∠PCB=∠DBC。∵C=2，sin∠BCP=∴，解得：DC=2。∴由勾股定理得：BD=4。∴点B到AC的距离为4。（3）如图，连接AN，在Rt△ACN中，，又CD=2，∴AD=AC﹣CD=5﹣2=3。∵BD∥CP，∴△ABD∽△AC

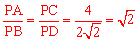（2）由cos∠CPQ=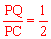，求出∠CPQ=60°，同理求出∠PDQ=45°。由圆周角定理，得出

∠CAQ=∠CPQ=60°，∠PBQ=∠PDQ=45°，求出∠PBD=90°，求出∠ABE=45°根据三角形的内角和定理求出即可。

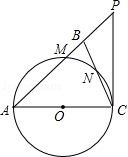
4.（2012四川广安9分）如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．

（1）求证：直线CP是⊙O的切线．

（2）若BC=2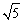，sin∠BCP=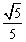，求点B到AC的距离．

（3）在第（2）的条件下，求△ACP的周长．

【答案】解：（1）∵∠ABC=∠ACB且∠CAB=2∠BCP，在△ABC中，∠ABC+∠BAC+∠BCA=180°，

∴2∠BCP+2∠BCA=180°。

∴∠BCP+∠BCA=90°，即∠PCA=90°。

又∵AC是⊙O的直径，∴直线CP是⊙O的切线。

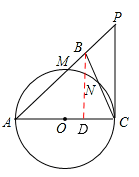
（2）如图，作BD⊥AC于点D，

∵PC⊥AC，∴BD∥PC。∴∠PCB=∠DBC。

∵C=2，sin∠BCP=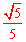

∴，解得：DC=2。

∴由勾股定理得：BD=4。∴点B到AC的距离为4。

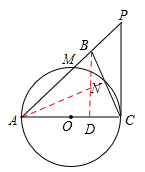
（3）如图，连接AN，

在Rt△ACN中，，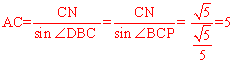

又CD=2，∴AD=AC﹣CD=5﹣2=3。

∵BD∥CP，∴△ABD∽△ACP。

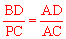∴，即。∴。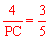

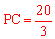在Rt△ACP中，。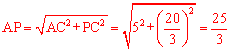

∴△ACP的周长为。

【考点】切线的判定和性质，三角形内角和定理，等腰三角形的性质，勾股定理，相似三角形的判定和性质，锐角三角函数定义。

【分析】（1））根据∠ABC=∠AC且∠CAB=2∠BCP，在△ABC中∠ABC+∠BAC+∠BCA=180°，得到2∠BCP+2∠BCA=180°，从而得到∠BCP+∠BCA=90°，证得直线CP是⊙O的切线。

（2）作BD⊥AC于点D，得到BD∥PC，从而利用求得DC=2，再根据勾股定理求得点B到AC的距离为4。

（3）先求出AC的长度，然后由BD∥PC求得△ABD∽△ACP，利用比例线段关系求得CP的长度，再由勾股定理求出AP的长度，从而求得△ACP的周长。

5.（2012四川达州7分）如图，C是以AB为直径的⊙O上一点，过O作OE⊥AC于点E，过点A作

⊙O的切线交OE的延长线于点F，连结CF并延长交BA的延长线于点P.

（1）求证：PC是⊙O的切线.

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页