圆形练习题及答案（三）

概要：根据锐角三角函数的定义求出AE及BE的长，在Rt△ADE中利用锐角三角函数的定义即可得出AD的长。②由三角形内角和定理求出∠AOE的度数，再根据OA=OB可知求出△AOE的面积，由即可得出结论。7.（2012四川德阳14分）如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O 的切线交直线AC于点D，点E为CH的中点，连结并延交BD于点F，直线CF交AB的延长线于G.⑴求证：AE·FD=AF·EC；⑵求证：FC=FB；⑶若FB=FE=2，求⊙O 的半径r的长.【答案】（1）证明：∵BD是⊙O的切线，∴∠DBA=90°。∵CH⊥AB，∴CH∥BD。∴△AEC∽△AFD。∴。∴AE•FD=AF•EC。（2）证明：∵CH∥BD，∴△AEC∽△AFD，△AHE∽△ABF。∴。∵CE=EH（E为CH中点），∴BF=DF。∵AB为⊙O的直径，∴∠ACB=∠DCB=90°。∴CF=DF=

【考点】切线的性质，平行的判定和性质，圆周角定理，锐角三角函数定义，特殊角的三角函数值，三角形内角和定理，扇形面积的计算。

【分析】（1）连接OE，由切线的性质可知，OE⊥CD，再根据AD⊥CD可知AD∥OE，故∠DAE=∠AEO，

再由OA=OE可知∠EAO=∠AEO，故∠DAE=∠EAO，故可得出结论。

（2）①根据∠ABE=60°求出∠EAO的度数，进而得出∠DAE的度数，再根据锐角三角函数的定

义求出AE及BE的长，在Rt△ADE中利用锐角三角函数的定义即可得出AD的长。

②由三角形内角和定理求出∠AOE的度数，再根据OA=OB可知求

出△AOE的面积，由即可得出结论。

7.（2012四川德阳14分）如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O 的切线交直线AC于点D，点E为CH的中点，连结并延交BD于点F，直线CF交AB的延长线于G.

⑴求证：AE·FD=AF·EC；

⑵求证：FC=FB；

⑶若FB=FE=2，求⊙O 的半径r的长.

【答案】（1）证明：∵BD是⊙O的切线，∴∠DBA=90°。

∵CH⊥AB，∴CH∥BD。∴△AEC∽△AFD。

∴。∴AE•FD=AF•EC。

（2）证明：∵CH∥BD，∴△AEC∽△AFD，△AHE∽△ABF。∴。

∵CE=EH（E为CH中点），∴BF=DF。

∵AB为⊙O的直径，∴∠ACB=∠DCB=90°。∴CF=DF=BF，即CF=BF。

（3）解：∵BF=CF=DF（已证），EF=BF=2，∴EF=FC。∴∠FCE=∠FEC。

∵∠AHE=∠CHG=90°，∴∠FAH+∠AEH=90°，∠G+∠GCH=90°。

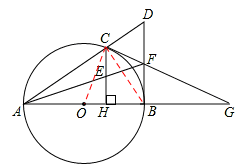∵∠AEH=∠CEF，∴∠G=∠FAG。∴AF=FG。

∵FB⊥AG，∴AB=BG。

连接OC，BC，

∵BF切⊙O于B，∴∠FBC=∠CAB。

∵OC=OA，CF=BF，

∴∠FCB=∠FBC，∠OCA=∠OAC

∴∠FCB=∠CAB。

∵∠ACB=90°，∴∠ACO+∠BCO=90°。∴∠FCB+∠BCO=90°，即OC⊥CG。

∴CG是⊙O切线。

∵GBA是⊙O割线，FB=FE=2，由切割线定理得：（2+FG）2=BG×AG=2BG2，

【注，没学切割线定理的可由△AGC∽△CGB求得】

在Rt△BFG中，由勾股定理得：BG2=FG2﹣BF2，∴FG2﹣4FG﹣12=0。

解得：FG=6，FG=﹣2（舍去）。

由勾股定理得：AB=BG=。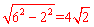

∴⊙O的半径r是。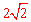

【考点】切线的判定和性质，等腰三角形判定和的性质，直角三角形斜边上的中线性质，勾股定理，圆周角定理，切割线定理，相似三角形的判定和性质。

【分析】（1）由BD是⊙O的切线得出∠DBA=90°，推出CH∥BD，证△AEC∽△AFD，得出比例式即可。

（2）证△AEC∽△AFD，△AHE∽△ABF，推出BF=DF，根据直角三角形斜边上中线性质得出CF=DF=BF即可。

（3）求出EF=FC，求出∠G=∠FAG，推出AF=FG，求出AB=BG，连接OC，BC，求出∠FCB=∠CAB推出CG是⊙O切线，由切割线定理（或△AGC∽△CGB）得出（2+FG）2=BG×AG=2BG2，在Rt△BFG中，由勾股定理得出BG2=FG2﹣BF2，推出FG2﹣4FG﹣12=0，求出FG即可，从而由勾股定理求得AB=BG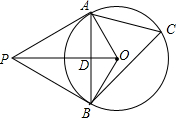

的长，从而得到⊙O的半径r。

8.（2012四川绵阳12分）如图，PA、PB分别切⊙O于A、B，连接PO、AB相交于D，C是⊙O上一点，∠C=60°。

（1）求∠APB的大小；

（2）若PO=20cm，求△AOB的面积。

【考点】切线的性质，圆周角定理，多边形内角和定理，线段垂直平分线的判定和性质，锐角三角函数定义，特殊角的三角函数值。

【分析】（1）由PA、PB分别切⊙O于A、B，由切线的性质，即可得OA⊥PA，OB⊥PB，又由圆周角定理，求得∠AOB的度数，继而求得∠APB的大小。

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页