圆形练习题及答案（三）

概要：直线l的解析式【答案】（1）证明：连接PB，∵直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，∴∠APB=∠DPO=×180°=60°，∠ABO=∠POD=90°。∵PA=PB，∴△PAB是等边三角形。∴AB=PA，∠BAO=60°，∴AB=OP，∠BAO=∠OPD。在△POD和△ABO中，∵∠OPD=∠BAO，OP=BA ，∠POD=∠ABO ，∴△POD≌△ABO（ASA）。（2）解：由（1）得△POD≌△ABO，∴∠PDO=∠AOB。∵∠AOB=∠APB=×60°=30°，∴∠PDO=30°。∴OP=OD•tan30°=3×。∴点P的坐标为：（－，0）。∵点P，D在直线y=kx+b上，∴，解得：。∴直线l的解析式为：y=x+3。【考点】圆周角定理

（2）由切线长定理，可求得∠APO的度数，继而求得∠AOP的度数，易得PO是AB的垂直平分线，然后利用三角函数的性质，求得AD与OD的长，从而求得答案。

9.（2012四川凉山8分）如图，已知直径为OA的⊙P与x轴交于O、A两点，点B、C把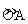三等分，连接PC并延长PC交y轴于点D（0，3）．

（1）　　　求证：△POD≌△ABO；

（2）　　　若直线l：y=kx+b经过圆心P和D，求直线l的解析式

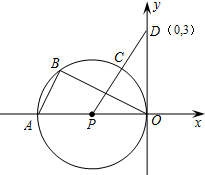
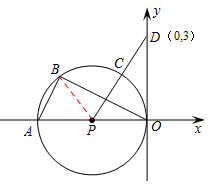
【答案】（1）证明：连接PB，

∵直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，

∴∠APB=∠DPO=×180°=60°，∠ABO=∠POD=90°。

∵PA=PB，∴△PAB是等边三角形。

∴AB=PA，∠BAO=60°，

∴AB=OP，∠BAO=∠OPD。

在△POD和△ABO中，

∵∠OPD=∠BAO，OP=BA ，∠POD=∠ABO ，　

∴△POD≌△ABO（ASA）。

（2）解：由（1）得△POD≌△ABO，∴∠PDO=∠AOB。

∵∠AOB=∠APB=×60°=30°，∴∠PDO=30°。

∴OP=OD•tan30°=3×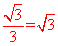。∴点P的坐标为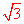：（－，0）。

∵点P，D在直线y=kx+b上，

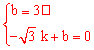∴，解得：。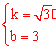

∴直线l的解析式为：y=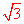x+3。

【考点】圆周角定理，全等三角形的判定，锐角三角函数定义，直线上点的坐标与方程的关系。

【分析】（1）首先连接PB，由直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，可求得∠APB=∠DPO=60°，∠ABO=∠POD=90°，即可得△PAB是等边三角形，可得AB=OP，然后由ASA，即可判定：△POD≌△ABO。

（2）易求得∠PDO=30°，由OP=OD•tan30°，即可求得点P的坐标，然后利用待定系数法，即可求得直线l的解析式。

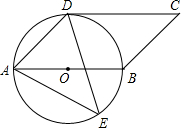
10.（2012四川巴中10分）如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O

上一点，且∠AED=45°。

（1）判断CD与⊙O的位置关系，并说明理由；

（2）若⊙O的半径为6cm，AE=10cm，求∠ADE的正弦值。

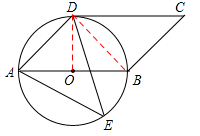
【答案】解：（1）连接BD，OD，

∵AB是直径，∴∠ADB=90°。

∵∠ABD=∠E=45°，∴∠DAB=45°，则AD=BD。

∴△ABD是等腰直角三角形。∴OD⊥AB。

又∵DC∥AB，∴OD⊥DC，∴CD与⊙O相切。

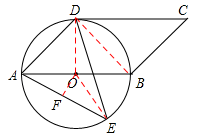
（2）过点O作OF⊥AE，连接OE，

则AF=

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页