圆形练习题及答案（三）

概要：，∴∠GDP=∠GPD。∴GP=GD。所以结论②正确。∵直径AB⊥CE，∴A为的中点，即。又∵点C是的中点，∴。∴。∴∠CAP=∠ACP。∴AP=CP。又∵AB为圆O的直径，∴∠ACQ=90°。∴∠PCQ=∠PQC。∴PC=PQ。∴AP=PQ，即P为Rt△ACQ斜边AQ的中点。∴P为Rt△ACQ的外心。所以结论③正确。④如图，连接CD，∵，∴∠B=∠CAD。又∠ACQ=∠BCA，∴△ACQ∽△BCA。∴，即AC2=CQ•CB。∵，∴∠ACP=∠ADC。又∠CAP=∠DAC，∴△ACP∽△ADC。∴，即AC2=AP•AD。∴AP•AD=CQ•CB。所以结论④正确。则正确的选项序号有②③④。7.（2012四川达州

∴∠BAD与∠ABC不一定相等。所以结论①错误。

②∵GD为圆O的切线，∴∠GDP=∠ABD。

又∵AB为圆O的直径，∴∠ADB=90°。

∵CE⊥AB，∴∠AFP=90°。∴∠ADB=∠AFP。

又∵∠PAF=∠BAD，∴∠ABD=∠APF。

又∵∠APF=∠GPD，∴∠GDP=∠GPD。∴GP=GD。所以结论②正确。

∵直径AB⊥CE，

∴A为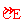的中点，即。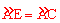

又∵点C是的中点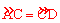，∴。∴。∴∠CAP=∠ACP。∴AP=CP。

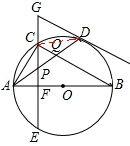又∵AB为圆O的直径，∴∠ACQ=90°。∴∠PCQ=∠PQC。∴PC=PQ。

∴AP=PQ，即P为Rt△ACQ斜边AQ的中点。

∴P为Rt△ACQ的外心。所以结论③正确。

④如图，连接CD，

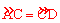∵，∴∠B=∠CAD。又∠ACQ=∠BCA，∴△ACQ∽△BCA。

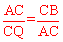∴，即AC2=CQ•CB。

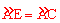∵，∴∠ACP=∠ADC。又∠CAP=∠DAC，∴△ACP∽△ADC。

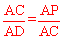∴，即AC2=AP•AD。

∴AP•AD=CQ•CB。所以结论④正确。

则正确的选项序号有②③④。

7.（2012四川达州3分）已知圆锥的底面半径为4，母线长为6，则它的侧面积是▲　　.（不取近似值）

【答案】24π。

【考点】圆锥的计算。

【分析】依题意知母线长=6，底面半径r=4，则由圆锥的侧面积公式得S=πrl=π×4×6=24π。

8.（2012四川广元3分）在同一平面上，⊙O外一点P到⊙O上一点的距离最长为6cm，最短为2cm，

则⊙O的半径为▲　cm

【答案】2。

【考点】点与圆的位置关系。

【分析】当点P在圆外时，直径=6 cm－2 cm =4cm，因而半径是2cm。

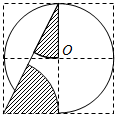
9.（2012四川凉山4分）如图，小正方形构成的网络中，半径为1的⊙O在格点上，则图中阴影部分两个小扇形的面积之和为　　▲　　（结果保留）。

【答案】。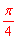

【考点】扇形面积的计算，直角三角形两锐角的关系。

【分析】如图，先根据直角三角形的性质求出∠ABC+∠BAC的值，再根据扇形的面积公式进行解答即可：

∵△ABC是直角三角形，∴∠ABC+∠BAC=90°。

∵两个阴影部分扇形的半径均为1，∴S阴影。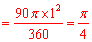

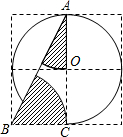
10.（2012四川巴中3分）有一个底面半径为3cm，母线长10cm的圆锥，则其侧面积是▲　　cm2

【答案】30π。

【考点】圆锥的计算。

【分析】直接根据公式：圆锥的侧面积=底面周长×母线长÷2计算即可：

∵底面圆的半径为3cm，母线长10cm，则底面周长=6πcm，

∴圆锥的侧面积=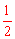

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页