圆形练习题及答案(九)
概要:弧,直径是圆中最大的弦.2.如图,点I为△ABC的内心,点O为△ABC的外心,∠O=140°,则∠I为()(A)140°(B)125°(C)130°(D)110°【提示】因点O为△ABC的外心,则∠BOC、∠A分别是所对的圆心角、圆周角,所以∠O=2∠A,故∠A=×140°=70°.又因为I为△ABC的内心,所以∠I=90°+∠A=90°+×70°=125°.【答案】B.【点评】本题考查圆心角与圆周角的关系,内心、外心的概念.注意三角形的内心与两顶点组成的角与另一角的关系式.3.如果正多边形的一个外角等于60°,那么它的边数为()(A)4(B)5(C)6(D)7【提示】正多边形的外角等于它的中心角,所以=60°,故n=6.【答案】C.【点评】此题考查正多边形的外角与中心角的关系.注意:正n边形的中心角为,且等于它的一个外角.4.如图,AB是⊙O的弦,点C是弦AB上一点,且BC︰CA=2︰1,连结OC并延长交⊙O于D,又DC=2厘米,OC=3厘米,则
圆形练习题及答案(九),http://www.jdxx5.com专题复习《圆》提高测试
(一)选择题:(每题2分,共20分)
1.有4个命题:
①直径相等的两个圆是等圆;②长度相等的两条弧是等弧;
③圆中最大的弧是过圆心的弧;④一条弦把圆分为两条弧,这两条弧不可能是等弧.
其中真命题是( )
(A)①③ (B)①③④ (C)①④ (D)①
【提示】长度相等的两弧不一定是等弧,故②不对;当弦是直径时,直径把圆分为两个半圆,它们是等弧,故④不对.
【答案】A.【点评】本题考查等圆、等弧、直线与弦的概念.注意:等弧是能互相重合的两条弧,直径是圆中最大的弦.
2.如图,点I为△ABC的内心,点O为△ABC的外心,∠O=140°,则∠I为( )
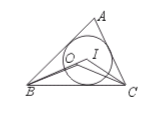 (A)140° (B)125° (C)130° (D)110°
(A)140° (B)125° (C)130° (D)110°
【提示】因点O为△ABC的外心,则∠BOC、∠A分别是 所对的圆心角、圆周角,所以∠O=2∠A,故∠A=
所对的圆心角、圆周角,所以∠O=2∠A,故∠A=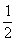 ×140°=70°.又因为I为△ABC的内心,所以
×140°=70°.又因为I为△ABC的内心,所以
∠I=90°+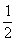 ∠A=90°+
∠A=90°+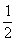 ×70°=125°.
×70°=125°.
【答案】B.
【点评】本题考查圆心角与圆周角的关系,内心、外心的概念.注意三角形的内心与两顶点组成的角与另一角的关系式.
3.如果正多边形的一个外角等于60°,那么它的边数为( )
(A)4 (B)5 (C)6 (D)7
【提示】正多边形的外角等于它的中心角,所以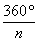 =60°,故n=6.
=60°,故n=6.
【答案】C.
【点评】此题考查正多边形的外角与中心角的关系.注意:正n边形的中心角为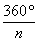 ,且等于它的一个外角.
,且等于它的一个外角.
4.如图,AB是⊙O的弦,点C是弦AB上一点,且BC︰CA=2︰1,连结OC并延长交⊙O于D,又DC=2厘米,OC=3厘米,则圆心O到AB的距离为( )
(A)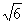 厘米 (B)
厘米 (B)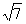 厘米 (C)2厘米 (D)3厘米
厘米 (C)2厘米 (D)3厘米
【提示】延长DO交⊙O于E,过点O作OF⊥AB于F,则CE=8厘米.
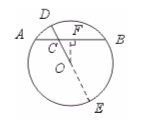 由相交弦定理,得DC·CE=AC·CB,所以AC·2 AC=2×8,
由相交弦定理,得DC·CE=AC·CB,所以AC·2 AC=2×8,
故AC=2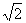 (厘米),从而BC=4
(厘米),从而BC=4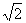 厘米.
厘米.
由垂径定理,得
AF=FB=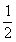 (2
(2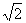 +4
+4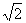 )=3
)=3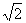 (厘米).
(厘米).
所以CF=3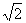 -2
-2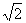
[1] [2] [3] [4] [5] [6] [7] [8] [9] 下一页

