圆形练习题及答案（二）

概要：2012贵州黔东南4分）如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=55°，则∠BCD的度数为（）A．35°B．45°C．55°D．75°【答案】A。【考点】圆周角定理，直角三角形两锐角关系。【分析】连接AD，∵AB是⊙O的直径，∴∠ADB=90°.∵∠ABD=55°，∴∠A=90°﹣∠ABD=35°。∴∠BCD=∠A=35°。故选A。3.（2012贵州黔南）已知两圆相外切，连心线长度是10厘米，其中一圆的半径为6厘米，则另一圆的半径是（）A．16厘米B．10厘米C．6厘米D．4厘米【答案】D。【考点】两圆的位置关系。【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。因此，由两圆相外切，连心线长度是10厘米，其中一圆的半径为6厘米可得另一圆的半径为10－6=4（厘米）

中考数学试题分类解析汇编专题11：圆

1、选择题

1.（2012贵州毕节3分）第三十奥运会将于2012年7月27日在英国伦敦开幕，奥运会旗图案有五个圆环组成，下图也是一幅五环图案，在这个五个圆中，不存在的位置关系是（　　）　

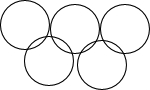
A外离　　B内切　　C外切　　D相交

【答案】B。

【考点】圆与圆的位置关系。

【分析】观察图形，五个等圆不可能内切，也不可能内含，并且有的两个圆只有一个公共点，即外切；有的两个圆没有公共点，即外离；有的两个圆有两个公共点，即相交。因此它们的位置关系有外切、外离、相交。故选B。

2.（2012贵州黔东南4分）如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=55°，则∠BCD的度数为（　　）　

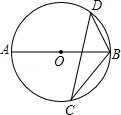
A．35°　　B．45°　　C．55°　　D．75°

【答案】A。

【考点】圆周角定理，直角三角形两锐角关系。

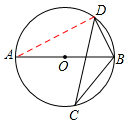
【分析】连接AD，

∵AB是⊙O的直径，∴∠ADB=90°.

∵∠ABD=55°，∴∠A=90°﹣∠ABD=35°。

∴∠BCD=∠A=35°。故选A。

3.（2012贵州黔南）已知两圆相外切，连心线长度是10厘米，其中一圆的半径为6厘米，则另一圆的半径是（　）　

A．16厘米　　B．10厘米　　C．6厘米　　D．4厘米

【答案】D。

【考点】两圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。因此，由两圆相外切，连心线长度是10厘米，其中一圆的半径为6厘米可得另一圆的半径为10－6=4（厘米）。故选D。

4.（2012贵州黔南4分）如图，在⊙O中，∠ABC=500，则∠CAO等于（　　）　

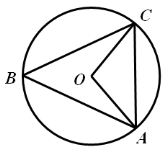
A．300　　B．400　　C．500　　D．600

【答案】B。

【考点】圆周角定理，等腰三角形的性质，三角形内角和定理。

【分析】∵∠ABC和∠AOC是弧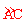所对的圆周角和圆心角，

　　　　∴∠AOC=2∠ABC=1000（同圆或等圆中同弧所对圆周角是圆心角的一半）。

　　　　∵OA=OC，∴∠OAC=∠OCA（等边对等角）。

　　　　∴根据三角形内角和定理，得∠CAO=。故选B。

5.（2012贵州黔西南4分）如图，⊙O是△ABC的外接圆，已知∠ABO＝40°，则∠ACB的大小为（　　）　

（A）40°　（B）30°　（C）50°　（D）60°

【答案】C。

【考点】等腰三角形的性质，圆周角定理；三角形内角和定理．

【分析】∵OA=OB，∠ABO＝40°，∴∠BAO=∠ABO=40°（等边对等角）。

∴∠AOB=100°（三角形内角和定理）。

∴∠ACB=50°（同弧所对圆周角是圆心角的一半）。故选C。

7.（2012贵州铜仁4分）小红要过生日了，为了筹备生日聚会，准备自己动手用纸板制作一个底面半径为9cm，母线长为30cm的圆锥形生日礼帽，则这个圆锥形礼帽的侧面积为（　　）　

A．270πcm2　　B．540πcm2　　C．135πcm2　　D．216πcm2

【答案】A。

【考点】圆锥的计算。

【分析】直接应用侧面积公式计算即可：圆锥形礼帽的侧面积=π×9×30=270πcm2。故选A。

8.（2012贵州遵义3分）如图，半径为1cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为（　　）　

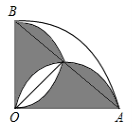
A．πcm2　　　B．

[1] [2] [3] [4] [5] [6] [7]  下一页