圆形练习题及答案（三）

概要：re4;∠FCO=∠FAO=90°。又∵OC是⊙O的半径，∴PC是⊙O的切线。（2）∵PC是⊙O的切线，∴∠PCO=90°。而∠FPA=∠OPC，∠PAF=90°，∴△PAF∽△PCO 。∴。∵CO=OA=，AF=1，∴PC=PA 。设PA=x，则PC=在Rt△PCO中，由勾股定理得，，解得：。∴PC。【考点】切线的判定和性质，垂径定理，圆周角定理，相似三角形的判定和性质，勾股定理。【分析】（1）连接OC，根据垂径定理，利用等角代换可证明∠FAC=∠FCA，然后根据切线的性质得出∠FAO=90°，然后即可证明结论。（2）先证明△PAF∽△PCO，利用相似三角形的性质得出PC与PA的关系，在Rt△PCO中，利用勾股定理可得出x的值，从而也可得出PC得长。6.（2012四川广元9分）如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD（1）求证：AE平分∠DAC；（2）若AB=3，∠ABE=60°，①求A

（2）若AF=1，OA=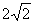，求PC的长.

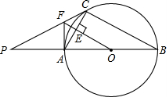
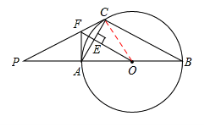
【答案】解：（1）证明：连结OC，

∵OE⊥AC，∴AE=CE。∴FA=FC。

∴∠FAC=∠FCA。

∵OA=OC，∴∠OAC=∠OCA。

∴∠OAC+∠FAC=∠OCA+∠FCA，即∠FAO=∠FCO。

∵FA与⊙O相切，且AB是⊙O的直径，∴FA⊥AB。∴∠FCO=∠FAO=90°。

又∵OC是⊙O的半径，∴PC是⊙O的切线。

（2）∵PC是⊙O的切线，∴∠PCO=90°。

而∠FPA=∠OPC，∠PAF=90°，∴△PAF∽△PCO 。∴。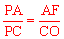

∵CO=OA=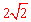，AF=1，∴PC=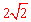PA 。

设PA=x，则PC=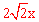

在Rt△PCO中，由勾股定理得，，解得：。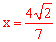

∴PC。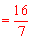

【考点】切线的判定和性质，垂径定理，圆周角定理，相似三角形的判定和性质，勾股定理。

【分析】（1）连接OC，根据垂径定理，利用等角代换可证明∠FAC=∠FCA，然后根据切线的性质得出∠FAO=90°，然后即可证明结论。

（2）先证明△PAF∽△PCO，利用相似三角形的性质得出PC与PA的关系，在Rt△PCO中，利用勾股定理可得出x的值，从而也可得出PC得长。

6.（2012四川广元9分）如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD

⊥CD

（1）求证：AE平分∠DAC；

（2）若AB=3，∠ABE=60°，

①求AD的长；②求出图中阴影部分的面积。

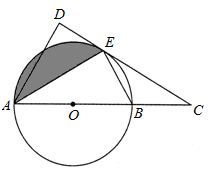
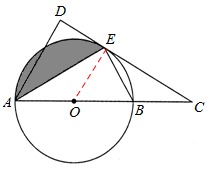
【答案】解：（1）证明：连接OE。

∵CD是⊙O的切线，∴OE⊥CD。

∵AD⊥CD，∴AD∥OE。∴∠DAE=∠AEO。

∵OA=OE，∴∠EAO=∠AEO。

∴∠DAE=∠EAO。∴AE平分∠DAC。
（2）①∵AB是⊙O的直径，∴∠AEB=90°。

∵∠ABE=60°，∴∠EAO=30°。∴∠DAE=∠EAO=30°。

∵AB=3，∴在Rt△ABE中，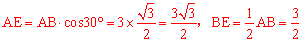

在Rt△ADE中，∵∠DAE=30°，AE= ，∴。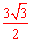

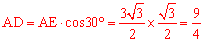②∵∠EAO=∠AEO=30°，∴。

∵OA=OB，∴。

∴

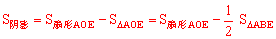
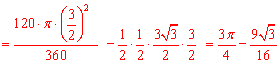
上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页