圆形练习题及答案（六）

概要：根据这个等式可即可求出CD。【没有学习切割线定理的，可连接BC，根据直径所对圆周角是直角的圆周角定理知∠ADB=900，从而根据△BCD∽△ACB得对应边成比例而求出CD。】4. （江苏省苏州市2003年7分）如图1，⊙O的直径为AB，过半径OA的中点G作弦CE⊥AB，在上取一点D，分别作直线CD、ED，交直线AB于点F、M。（1）求∠COA和∠FDM的度数；（2）求证：△FDM∽△COM；（3）如图2，若将垂足G改取为半径OB上任意一点，点D改取在上，仍作直线CD、ED，分别交直线AB于点F、M。试判断：此时是否仍有△FDM∽△COM？证明你的结论。【答案】解：（1）∵AB为直径，CE⊥AB，∴，CG=EG。在Rt△COG中，∵OG=OC，∴∠OCG=30°。∴∠COA=60°。又∵∠CDE的度数=的度数= 的度数=∠COA的度数=60°，∴∠FDM=180°－∠CDE=120°。（2）证明：∵∠COM=180°－∠COA=120&d

【答案】解：∵AB是⊙O直径，BC是⊙O的切线，∴BC⊥AB。

∴在Rt△ABC中，。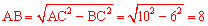

∵CA是⊙O的割线，∴CD•CA=BC2。

∴CD×10=62，∴CD=3.6。

【考点】切线的性质，切割线定理，勾股定理。

【分析】由AB是⊙O直径，BC是⊙O的切线可以得到BC⊥AB，利用勾股定理在Rt△ABC中可以求出AB的长，又由CA是⊙O的割线看得到BC2=CD•CA，根据这个等式可即可求出CD。

【没有学习切割线定理的，可连接BC，根据直径所对圆周角是直角的圆周角定理知∠ADB=900，从而根据△BCD∽△ACB得对应边成比例而求出CD。】

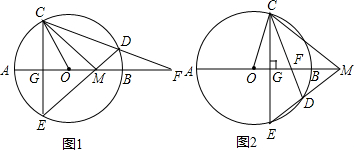
4. （江苏省苏州市2003年7分）如图1，⊙O的直径为AB，过半径OA的中点G作弦CE⊥AB，在上取一点D，分别作直线CD、ED，交直线AB于点F、M。

（1）求∠COA和∠FDM的度数；

（2）求证：△FDM∽△COM；

（3）如图2，若将垂足G改取为半径OB上任意一点，点D改取在上，仍作直线CD、ED，分别交直

线AB于点F、M。试判断：此时是否仍有△FDM∽△COM？证明你的结论。

【答案】解：（1）∵AB为直径，CE⊥AB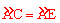，∴，CG=EG。

在Rt△COG中，∵OG=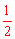OC，∴∠OCG=30°。∴∠COA=60°。

又∵∠CDE的度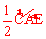数=的度数= 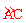的度数=∠COA的度数=60°，

∴∠FDM=180°－∠CDE=120°。

（2）证明：∵∠COM=180°－∠COA=120°，∴∠COM=∠FDM。

在Rt△CGM和Rt△EGM中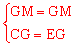，，∴Rt△CGM≌Rt△EGM（HL）。

∴∠GMC=∠GME。

又∵∠DMF=∠GME，∴∠GMC=∠DMF。∴△FDM∽△COM。

（3）结论仍成立。证明如下：

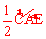∵∠EDC的度数=的度数=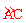的度数=∠COA的度数，

∴∠FDM=180°－∠COA=∠COM。

∵AB为直径，∴CE⊥AB。

在Rt△CGM和Rt△EGM中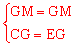，∴Rt△CGM≌Rt△EGM（HL）。

∴∠GMC=∠GME。∴△FDM∽△COM。

【考点】圆周角定理，锐角三角函数，特殊角的三角函数值，线段垂直平分线的性质，直角三角形两锐角的关系，平角定义，直角三角形全等的判定和性质，垂径定理，相似三角形的判定。

【分析】（1）由于CG⊥OA，根据垂径定理可得出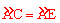，，那么根据圆周角定理可得出∠CDE=∠COA，在Rt△COG中，可根据OG是半径的一半得出∠AOC是60°，那么就能得出∠FDM=180°－∠CDE=120°。

（2）在（1）中根据垂径定理得出OA是CE的垂直平分线，那么△CMG和△BMG就应该全等，可得出∠CMA=∠EMG，也就可得出∠CMO=∠FMD，在（1）中已经证得∠AOC=∠EDC=60°，那么∠COM=∠MDF，因此两三角形相似。

（3）可按（2）的方法得出∠DMF=∠CMO，关键是再找出一组对应角相等，还是用垂径定理来求，根据垂径定理我们可得出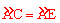，那么∠AOC=∠EDC，根据等角的余角相等即可得出∠COM=∠FDM，由此可证出两三角形相似。

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页