圆形练习题及答案(六)
概要:该扇形的半径是 ▲ .【答案】2。【考点】弧长的计算。【分析】根据弧长的公式,得,即该扇形的半径为2。三、解答题1. (2001江苏苏州6分)如图,已知AB是半圆O的直径,AP为过点A的半圆的切线。在上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E.连接BD,交CE于点F。(1)当点C为的中点时(如图1),求证:CF=EF;(2)当点C不是 的中点时(如图2),试判断CF与EF的相等关系是否保持不变,并证明你的结论。【答案】解:(1)证明:∵DA是切线,AB为直径,∴DA⊥AB。∵点C是的中点,且CE⊥AB,∴点E为半圆的圆心。又∵DC是切线,∴DC⊥EC。又∵CE⊥AB,∴四边形DAEC是矩形。∴CD∥AO,CD=AD。∴,即EF=AD=EC。∴F为EC的中点,CF=EF。(2)CF=EF保持不变。证明如下:如图,连接BC,并延长BC交AP于G点,连接AC,∵AD、DC是半圆O的切线,∴DC=DA。∴∠DAC=
圆形练习题及答案(六),http://www.jdxx5.com,根据扇形的弧长公式可计算
 出弧长为:
出弧长为:
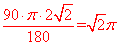 。
。
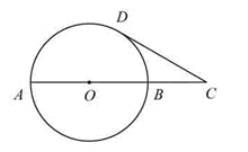
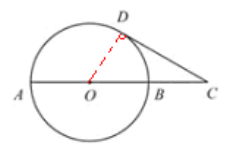
9. (江苏省苏州市2011年3分)如图,已知AB是⊙O的一条直径,延长AB至C点,使得AC=3BC,
CD与⊙O相切,切点为D.若CD=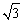 ,则线段BC的长度等于 ▲ .
,则线段BC的长度等于 ▲ .

【答案】1。
【考点】圆的切线性质,勾股定理。
【分析】连接OD, 则由圆的切线 性质得OD⊥CD,
性质得OD⊥CD,
由AC=3BC有OC=2BC=2OB。
∴Rt△CDO中, 根据勾股定理有
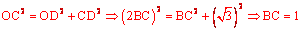 。
。
10. (2012江苏苏州3分)已知扇形的圆心角为45°,弧长等于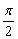 ,则该扇形的半径是 ▲ .
,则该扇形的半径是 ▲ .
【答案】2。
【考点】弧长的计算。
【分析】根据弧长的公式 ,得
,得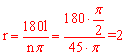 ,即该扇形的半径为2。
,即该扇形的半径为2。
三、解答题
1. (2001江苏苏州6分)如图,已知AB是半圆O的直径,AP为过点A的半圆的切线。在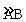 上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E.连接BD,交CE于点F。
上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E.连接BD,交CE于点F。
(1)当点C为 的中点时(如图1),求证:CF=EF;
的中点时(如图1),求证:CF=EF;
(2)当点C不是 的中点时(如图2),试判断CF与EF的相等关系是否保持不变,并证明你的结论。
的中点时(如图2),试判断CF与EF的相等关系是否保持不变,并证明你的结论。
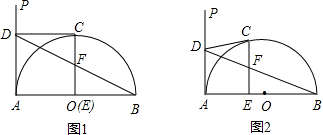
【答案】解:(1)证明:∵DA是切线,AB为直径,∴DA⊥AB。
∵点C是 的中点,且CE⊥AB,∴点E为半圆的圆心。
的中点,且CE⊥AB,∴点E为半圆的圆心。
又∵DC是切线,∴DC⊥EC。
又∵CE⊥AB,∴四边形DAEC是矩形。
∴CD∥AO,CD=AD。∴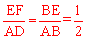 ,即EF=
,即EF=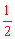 AD=
AD=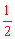 EC。
EC。
∴F为EC的中点,CF=EF。
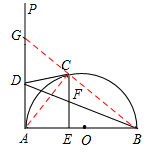 (2)CF=EF保持不变。证明如下:
(2)CF=EF保持不变。证明如下:
如图,连接BC,并延长BC交AP于G点,连接AC,
∵AD、DC是半圆O的切线,∴DC=DA。
∴∠DAC=∠DCA。
∵AB是直径,∴∠ACB=90°。∴∠ACG=90°。
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页

