圆形练习题及答案（六）

概要：O1中，∠B=∠D，∠D=∠FCE，∴∠FCE=∠B。∴AB∥EC。（2）仍有AB∥EC。证明如下：∵四边形ABCD是⊙O1的内接四边形，∴∠FBA=∠FDC。∵BC为⊙O2的切线，∴∠FCE=∠FDC。∴∠FCE=∠FBA。∴AB∥EC。【考点】弦切角定理，圆周角定理，圆内接四边形的性质，相似三角形的判定，平行线的判定。【分析】（1）①在△FDC与△FCE中，由弦切角定理得：∠D=∠FCE，已知公共角∠F，由此可判定两三角形相似。②根据平行线的判定，只需证明∠FCE=∠B；①中证得∠D=∠FCE，而⊙O1中，根据圆周角定理，可得∠D=∠B，将等角代换可得出∠B=∠FCE，由此得证。（2）根据平行线的判定，只需证明∠FCE=∠FBA，思路同（1）②，根据圆内接四边形的性质，得∠FBA=∠FDC；由弦切角定理，得∠FCE=∠FDC，将等

5. （江苏省苏州市2004年6分）如图，⊙O2与⊙O1 的弦BC切于C点，两圆的另一个交点为D，动点A在⊙O1，直线AD与⊙O2交于点E，与直线BC交于点 F 。

（1）如图1，当A在弧CD上时，求证：

①△FDC∽△FCE；

② AB∥EC ；

（2）如图2，当A在弧BD上时，是否仍有AB∥EC？请证明你的结论。　

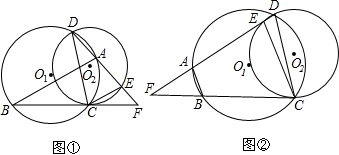
【答案】解：（1）证明：①∵BC为⊙O2的切线，∴∠D=∠FCE。

又∵∠F=∠F，∴△FDC∽△FCE。

②在⊙O1中，∠B=∠D，∠D=∠FCE，

∴∠FCE=∠B。∴AB∥EC。
（2）仍有AB∥EC。证明如下：

∵四边形ABCD是⊙O1的内接四边形，∴∠FBA=∠FDC。

∵BC为⊙O2的切线，∴∠FCE=∠FDC。∴∠FCE=∠FBA。∴AB∥EC。

【考点】弦切角定理，圆周角定理，圆内接四边形的性质，相似三角形的判定，平行线的判定。

【分析】（1）①在△FDC与△FCE中，由弦切角定理得：∠D=∠FCE，已知公共角∠F，由此可判定两三角形相似。②根据平行线的判定，只需证明∠FCE=∠B；①中证得∠D=∠FCE，而⊙O1中，根据圆周角定理，可得∠D=∠B，将等角代换可得出∠B=∠FCE，由此得证。

（2）根据平行线的判定，只需证明∠FCE=∠FBA，思路同（1）②，根据圆内接四边形的性质，得∠FBA=∠FDC；由弦切角定理，得∠FCE=∠FDC，将等角代换后可证得所求的结论。

6. （江苏省苏州市2005年6分）如图，AB是⊙O的直径，BC是⊙O的切线，D是⊙O上的一点，且AD∥CO。

（1）求证：△ADB∽△OBC；

（2）若AB=2，BC=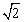，求AD的长。（结果保留根号）

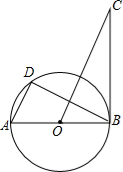
【答案】解：（1）∵AD∥OC，∴∠A=∠COB。

又∵AB是直径，BC是⊙O的切线，∴∠D=∠OBC=90°。∴△ADB∽△OBC。
（2）在Rt△OBC中，OB=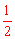AB=1，B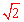C=，∴OC=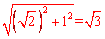

∵△ADB∽△OBC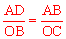，∴，即。∴。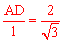

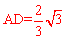【考点】相似三角形的判定和性质，圆周角定理，切线的性质，勾股定理。

【分析】（1）根据平行线的性质得∠A=∠COB，根据直径所对的圆周角是直角得∠D=∠OBC，就可以判定△ADB∽△OBC。

（2）根据相似三角形的对应边成比例可以计算出OC的长。

7. （江苏省苏州市2006年7分） 如图①，△ABC内接于⊙O，且∠ABC＝∠C，点D在弧BC上运动．过点D作DE∥BC．DE交直线AB于点E，连结BD．

　 (1)求证：∠ADB=∠E；　 (2)求证：AD2=AC·AE；

　 (3)当点D运动到什么位置时，△DBE∽△ADE请你利用图②进行探索和证明

【答案】解：（1）证明：∵DE∥BC，∴∠ABC=∠E。

∵∠ADB，∠C都是AB所对的圆周角，∴∠ADB=∠C。

又∠ABC=∠C，∴∠ADB=∠E。
（2）证明：∵∠ADB=∠E，∠BAD=∠DAE，∴△ADB∽△AED。

∴，即AD2=AB•AE。

又∵∠ABC=∠C，∴AB=AC，∴AD2=AC•AE。

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页