圆形练习题及答案(六)
概要:切线,∴AP⊥AB。又∵CE⊥AB,∴CE∥AP。∴△BCF∽△BGD,△BEF∽△BAD。∴。∵GD=AD,∴CF=EF。【考点】探究型,圆的综合题,切线的性质,矩形的判定和性质,平行线分线段成比例定理,等腰三角形的判定,相似三角形的判定和性质。【分析】(1)由题意得DA⊥AB,点E为半圆的圆心,DC⊥EC,可得四边形DAEC是矩形,即可得出 ,即可得EF与EC的关系,可知CF=EF。(2)连接BC,并延长BC交AP于G点,连接AC,由切线长定理可得DC=DA,∠DAC=∠DCA,由角度代换关系可得出∠DGC=∠DCG,即可得GD=DC=DA,由已知可得CE∥AP,所以 ,即可知CF=EF。2. (江苏省苏州市2002年7分)已知:⊙与⊙外切于点,过点的直线分别交⊙、⊙于点、,⊙的切线交⊙于点、,为⊙的弦,(1)如图(1),设弦交于点,求证:;(2)如图(2),当弦上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页
圆形练习题及答案(六),http://www.jdxx5.com∴∠DGC+∠DAC=∠DCA+∠DCG=90°。
∴∠DGC=∠DCG。
∴在△GDC中,GD=DC。
∵DC=DA,∴GD=DA。
∵AP是半圆O的切线,∴AP⊥AB。
又∵CE⊥AB,∴CE∥AP。∴△BCF∽△BGD,△BEF∽△BAD。
∴ 。
。
∵GD=AD,∴CF=EF。
【考点】探究型,圆的综合题,切线的性质,矩形的判定和性质,平行线分线段成比例定理,等腰三角形的判定,相似三角形的判定和性质。
【分析】(1)由题意得DA⊥AB,点E为半圆的圆心,DC⊥EC,可得四边形DAEC是矩形,即可得出 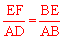 ,即可得EF与EC的关系,可知CF=EF。
,即可得EF与EC的关系,可知CF=EF。
(2)连接BC,并延长BC交AP于G点,连接AC,由切线长定理可得DC=DA,∠DAC=∠DCA,由角度代换关系可得出∠DGC=∠DCG,即可得GD=DC=DA,由已知可得CE∥AP,所以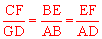 ,即可知CF=EF。
,即可知CF=EF。
2. (江苏省苏州市2002年7分)已知:⊙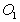 与⊙
与⊙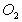 外切于点
外切于点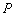 ,过点
,过点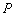 的直线分别交⊙
的直线分别交⊙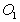 、⊙
、⊙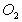 于点
于点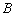 、
、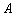 ,
, ⊙
⊙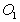 的切线
的切线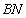 交⊙
交⊙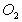 于点
于点 、
、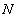 ,
,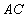 为⊙
为⊙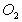 的弦,
的弦,
(1)如图(1),设弦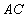 交
交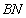 于点
于点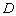 ,求证:
,求证: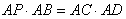 ;
;
(2)如图(2),当弦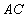
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页

