圆形练习题及答案(九)
概要:】本题考查等边三角形的面积的求法、内切圆半径的求法.注意:求三角形的内切圆的半径,通常用面积法.6.如图,⊙O的弦AB、CD相交于点P,PA=4厘米,PB=3厘米,PC=6厘米,EA切⊙O于点A,AE与CD的延长线交于点E,AE=2厘米,则PE的长为()(A)4厘米(B)3厘米(C)厘米(D)厘米【提示】由相交弦定理,得PA·PB=PD·PC.∴ 4×3=PD·6.∴ PD=2(厘米).由切割线定理,得AE2=ED·EC.∴ (2)2=ED ·(ED+2+6).解此方程得ED=2或ED=-10(舍去).∴ PE=2+2=4(厘米).【答案】A.【点评】本题考查相交弦定理、切割线定理.注意:应用相交弦定理、切割线定理往往建立方程,通过解方程求解.7.一个扇形的弧长为20??厘米,面积是240??厘米2,则扇形的圆心角是()(A)120°(B)150°(C)210°(D)240°【提示】设扇形的圆心角为n度,半径为R,则解方程组得【答案】B.【点评】本题考查扇形的弧长、面积公式.注
圆形练习题及答案(九),http://www.jdxx5.com=
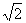 (厘米).
(厘米).
在Rt△COF中,OF=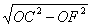 =
=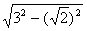 =
=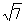 (厘米).
(厘米).
【答案】C.
【点评】本题考查相交弦定理、垂径定理.注意:在圆中求线段的长,往往利用相交弦定理、垂径定理进行线段的转换,再结合勾股定理建立等式.
5.等边三角形的周长为18,则它的内切圆半径是( )
(A)6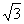 (B)3
(B)3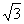 (C)
(C)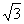 (D)
(D)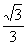
【提示】等边三角形的边长为6,则它的面积为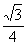 ×62=9
×62=9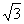 .又因为三角形的面积等于内切圆半径与三角形的周长的积的一半,所以9
.又因为三角形的面积等于内切圆半径与三角形的周长的积的一半,所以9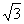 =
=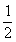 r·18(r为内切圆半径).
r·18(r为内切圆半径).
解此方程,得r=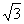 .
.
【答案】C.
【点评】本题考查等边三角形的面积的求法、内切圆半径的求法.注意:求三角形的内切圆的半径,通常用面积法.
6.如图,⊙O的弦AB、CD相交于点P,PA=4厘米,PB=3厘米,PC=6厘米,EA切⊙O于点A,AE与CD的延长线交于点E,AE=2 厘米,则PE的长为( )
厘米,则PE的长为( )
(A)4厘米 (B)3厘米 (C)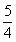 厘米 (D)
厘米 (D)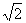 厘米
厘米
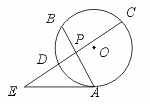
【提示】由相交弦定理,得PA·PB=PD·PC.
∴ 4×3=PD·6.
∴ PD=2(厘米).
由切割线定理,得 AE2=ED·EC.
∴ (2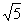 )2=ED ·(ED+2+6).解此方程得
)2=ED ·(ED+2+6).解此方程得
ED=2或ED=-10(舍去).
∴ PE=2+2=4(厘米).
【答案】A.
【点评】本题考查相交弦定理、切割线定理.注意:应用相交弦定理、切割线定理往往建立方程,通过解方程求解.
7.一个扇形的弧长为20??厘米,面积是240??厘米2,则扇形的圆心角是( )
(A)120° (B)150° (C)210° (D)240°
【提示】设扇形的圆心角为n度,半径为R,则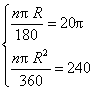 解方程组得
解方程组得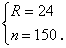
【答案】B.
【点评】本题考查扇形的弧长、面积公式.注意:应熟记扇形的弧长公式、扇形的面积公式.
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] 下一页

