圆形练习题及答案（九）

概要：e4; 四边形ACDB的面积为（2＋8）·8＝40（cm2）．【答案】40 cm2．【点评】本题考查直径的性质、中位线的判定与性质、切线的性质．注意：在圆中不要忽视直径这一隐含条件．17．如图，PA、PB、DE分别切⊙O于A、B、C，⊙O的半径长为6 cm，PO＝10 cm，则△PDE的周长是______．图中知，CM＝R＋8，MD＝R－8，【提示】连结OA，则OA⊥AP．在Rt△POA中，PA＝＝＝8（cm）．由切线长定理，得EA＝EC，CD＝BD，PA＝PB，∴ △PDE的周长为PE＋DE＋PD＝PE＋EC＋DC＋PD，＝PE＋EA＋PD＋DB＝PA＋PB＝16（cm）．【答案】16 cm．【点评】本题考查切线长定理、切线的性质、勾股定理．注意：在有关圆的切线长的计算中，往往利用切线长定理进行线段的转换．18．一个正方形和一个正六边形的外接圆半径相等，则此正方形与正六边形的面积之比为_______．【提示】设两正多边形的外接圆半径为R，则正方形面积为4×·R2＝2 R2，正六边形的面积为6×R2＝R2，所以它们的比为2 R2：R2＝4︰9．【答案】4︰9．【点评】本

【提示】设AC交⊙O于F，连结BF．

∵　 AB为⊙O的直径，

∴　 ∠AFB＝90°．

连结OE，则OE⊥CD，

∴　 AC∥OE∥BD．

∵　 点O为AB的中点，

∴　 E为CD的中点．

∴　 OE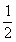＝（BD＋AC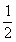）＝（8＋2）＝5（cm）．

∴　 AB＝2×5＝10（cm）．

在Rt△BFA中，AF＝CA－BD＝8－2＝6（cm），AB＝10 cm，

∴　 BF＝＝8（cm）．

∴　 四边形ACDB的面积为

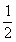（2＋8）·8＝40（cm2）．

【答案】40 cm2．

【点评】本题考查直径的性质、中位线的判定与性质、切线的性质．注意：在圆中不要忽视直径这一隐含条件．

17．如图，PA、PB、DE分别切⊙O于A、B、C，⊙O的半径长为6 cm，PO＝10 cm，

则△PDE的周长是______．

图中知，CM＝R＋8，MD＝R－8，

【提示】连结OA，则OA⊥AP．

在Rt△POA中，PA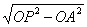＝＝＝8（cm）．

由切线长定理，得EA＝EC，CD＝BD，PA＝PB，

∴　 △PDE的周长为

PE＋DE＋PD

＝PE＋EC＋DC＋PD，

＝PE＋EA＋PD＋DB

＝PA＋PB＝16（cm）．

【答案】16 cm．

【点评】本题考查切线长定理、切线的性质、勾股定理．注意：在有关圆的切线长的计算中，往往利用切线长定理进行线段的转换．

18．一个正方形和一个正六边形的外接圆半径相等，则此正方形与正六边形的面积之比为_______．

【提示】设两正多边形的外接圆半径为R，则正方形面积为4×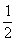·R2＝2 R2，正六边形的面积为6×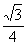R2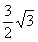＝R2，所以它们的比为2 R2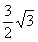：R2＝4︰9．

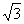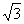【答案】4︰9．

【点评】本题考查正方形、正六边形的面积与外接圆的半径之间的关系．注意：正多边形的面积通常化为n个三角形的面积和．

19．如图，已知PA与圆相切于点A，过点P的割线与弦AC交于点B，与圆相交于点D、

E，且PA＝PB＝BC，又PD＝4，DE＝21，则AB＝______．

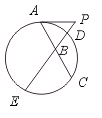
【提示】由切割线定理，得　 PA2＝PD·PE．

∴　 PA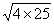＝＝10．

∴　 PB＝BC＝10．

∵　 PE＝PD＋DE＝25，

∴　 BE＝25－10＝15．

∴　 DB＝21－15＝6．

由相交弦定理，得　 AB·BC＝BE·BD．

∴　 AB·10＝15×6．

∴　 AB＝9．

【答案】9．

【点评】本题考查切割线定理与相交弦定理的应用，要观察图形，适当地进行线段间的转化．

20．如图，在□ABCD中，AB＝4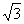

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9]  下一页