圆形练习题及答案(九)
概要:没有公共点时,这两个圆外离()【答案】×.【点评】两圆没有公共点时,既可以是外离,也可以是内含,所以原命题不成立.(四)解答题与证明题(共50分)26.(8分)如图,△ABC内接于⊙O,AB的延长线与过C点的切线GC相交于点D,BE与AC相交于点F,且CB=CE,求证:(1)BE∥DG;(2)CB2-CF2=BF·FE.【提示】(1)证明利用弦切角定理进行角之间的转化可证∠E=∠GCE;把(2)变形为CB2=CF2+BF·FE.∵ BF·FE=CF·AF,∴ CF2+BF·FE=CF2+CF·AF=CF(CF+AF)=CF·CA.即只要证CB2=CF·CA即可,只需证△CBF∽△CAB.【略证】(1)∵ CG为⊙O的切线,∴ ∠EBC=∠GCE.∵ CB=CE,∴ .∴ ∠EBC=∠E.∴ ∠E=∠GCE.∴ GC∥EB.(2)∵ ∠EBC=∠E=∠A,
圆形练习题及答案(九),http://www.jdxx5.com22.等腰三角形顶角平分线所在直线必过其外接圆的圆心( )
【答案】√.【点评】因为等腰三角形的顶角平分线垂直平分底边,根据垂径定理的推论知,顶角平分线所在直线必过圆心.
23.直角梯形的四个顶点不在同一个圆上( )
【答案】√.
【点评】若在同一个圆上,则对角互补,故四个角全为直角.所以假设不成立,原命题成立.
24.等边三角形的内心与外心重合( )
【答案】√.
【点评】等腰三角形的顶角的平分线也是对边的中线与高,因此等边三角形的内心与外心重合.
25.两圆没有公共点时,这两个圆外离( )
【答案】×.【点评】两圆没有公共点时,既可以是外离,也可以是内含,所以原命题不成立.
(四)解答题与证明题(共50分)
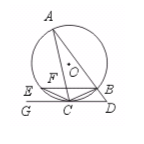
26.(8分)如图,△ABC内接于⊙O,AB的延长线与过C点的切线GC相交于点D,
BE与AC相交于点F,且CB=CE,求证:(1)BE∥DG;(2)CB2-CF2=BF·FE.
【提示】(1)证明利用弦切角定理进行角之间的转化可证∠E=∠GCE;把(2)变形为CB2=CF2+BF·FE.
∵ BF·FE=CF·AF,
∴ CF2+BF·FE=CF2+CF·AF
=CF(CF+AF)
=CF·CA.
即只要证CB2=CF·CA即可,只需证△CBF∽△CAB.
 【略证】(1)∵ CG为⊙O的切线,
【略证】(1)∵ CG为⊙O的切线,
∴ ∠EBC=∠GCE.
∵ CB=CE,∴ 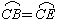 .
.
∴ ∠EBC=∠E.∴ ∠E=∠GCE.∴ GC∥EB.
(2)∵ ∠EBC=∠E=∠A,∠FCBO为公共角,
∴ △CBF∽△CAB.
∴ CB2=CF·CA=CF·(CF+AF)=CF2+CF·AF.
由相交弦定理,得 CF·FA=BF·FE,
∴ CB2=CF2+BF·FE.即 CB2-CF2=BF·FE.
【点评】对于形如a2=cd+ef的等式的证明较困难,因不易找到突破口.一般先把待证明的等式进行变形,以便于看出等式中线段之间的联系.如本题中,先把CF2移到等式的右边去,再结合相交弦定理找出了思路.
27.(8分)如图,⊙O表示一个圆形工件,图中标注了有关尺寸,且MB︰MA=1︰4,求工件半径的长.
【提示】把OM向两方延长,交⊙O于点C、D.设⊙O的半径为R,则可用相交弦定理求半径长.
【略解】把OM向两方延长,分别交⊙O于C、D两点.设⊙O的半径为R.
从图中知,AB=15 cm.
又 MB︰MA=1︰4,
∴ MB=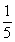 ×15=3(cm),MA=12 cm.
×15=3(cm),MA=12 cm.
从图中知,CM=R+8,MD=R-8,
 由相交弦定理,得 AM·BM=CM·MD.
由相交弦定理,得 AM·BM=CM·MD.
∴ 12×3=(R+8)(R-8).
解此方程,得 R=10或R=-10(舍去).
故工件的半径长为10 cm.
【点评】此题是一道实际问题,要善于把实际问题转化为数学问题,因在圆中,OM与AB相交,故向相交弦定理转化.
28.(8分)已知:如图(1),⊙O1与⊙O2相交于A、B两点,经过A点的直线分别交⊙O1、⊙O2于C、D两点(C、D不与B重合),连结BD,过点C作BD的平行线交⊙O1于点E,连BE.
(1)求证:BE是⊙O2的切线;
(2)如图(2),若两圆圆心在公共弦AB的同侧,其他条件不变,判断BE和⊙O2的位置关系(不要求证明).
【提示】(1)过B作⊙O2的直径BH,连结AB、AH,证∠EBH=90°.(2)用类似的方法去探求.
【证明】(1)连结AB,作⊙O2的直径BH,连结AH.
则 ∠ABH+∠H=90°,∠H=∠ADB,∠EBA=∠ECA.
 ∵ EC∥BD,
∵ EC∥BD,
∴ ∠ADB=∠ACE=∠EBA.
∴ ∠EBA+∠ABH=90°.
即 ∠EBH=90°.
∴ BE是⊙O2的切线.
(2)同理可知,BE仍是⊙O2的切线.

【点评】证明一与圆有公共点的直线是圆的切线的一般方法是过公共点作半径(或直径),再证直径与半径垂直,但此题已知条件中无90°的角,故作直径构造90°的角,再进行角的转换.同时两圆相交,通常作它们的公共弦,这样把两圆中的角都联系起来了.另外,当问题进行了变式时,要学会借鉴已有的思路解题.
29.(12分)如图,已知CP为⊙O的直径,AC切⊙O于点C,AB切⊙O于点D,并
与CP的延长线相交于点B,又BD=2 BP.
求证:(1)PC=3 PB;(2)AC=PC.
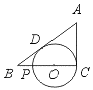
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] 下一页

