圆形练习题及答案(一)
概要:的公切线。∵是⊙的切线,∴。∴。∴。又∵,∴。又∵,∴。∴,即。【考点】相切两圆切线的性质,弦切角定理,切线长定理,等腰三角形的性质,对顶角的性质,相似三角形的判定和性质。【分析】(1)连结,过点作⊙与⊙的公切线。根据弦切角定理可得,由也是⊙的切线,根据切线长定理可得,从而根据等腰三角形等边对等角的性质,得到,由对顶角相等的性质,得到。又,从而,根据相似三角形的性质即可证明。(2)同(1)可以证明。3. (江苏省苏州市2003年7分)如图,已知AB是⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,AC=10,BC=6,求AB和CD的长。上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页
圆形练习题及答案(一),http://www.jdxx5.com的公切线
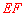 。
。
∵ 是⊙
是⊙ 的切线,∴
的切线,∴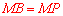 。
。
∴ 。
。
∴ 。
。
又∵ ,∴
,∴ 。
。
又∵ ,∴
,∴ 。
。
∴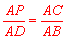 ,即
,即 。
。
【考点】相切两圆切线的性质,弦切角定理,切线长定理,等腰三角形的性质,对顶角的性质,相似三角形的判定和性质。
【分析】(1)连结 ,过点
,过点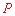 作⊙
作⊙ 与⊙
与⊙ 的公切线
的公切线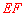 。根据弦切角定理可得
。根据弦切角定理可得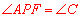 ,由
,由 也是⊙
也是⊙ 的切线,根据切线长定理可得
的切线,根据切线长定理可得 ,从而根据等腰三角形等边对等角的性质,得到
,从而根据等腰三角形等边对等角的性质,得到 ,由对顶角相等的性质,得到
,由对顶角相等的性质,得到 。又
。又 ,从而
,从而 ,根据相似三角形的性质即可证明。
,根据相似三角形的性质即可证明。
(2)同(1)可以证明。
3. (江苏省苏州市2003年7分)如图,已知AB是⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,AC=10,BC=6,求AB和CD的长。
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页

- 圆形练习题及答案(一)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
