圆形练习题及答案（一）

概要：g;ABC=∠E；由∠ADB，∠C都是AB所对的圆周角，得∠ADB=∠C；又∠ABC=∠C，因此∠ADB=∠E。（2）由∠ABC=∠C得AB=AC；由△ADB∽△AED得；即AD2=AB•AE=AC•AE。（3）点D运动到弧BC中点时，△DBE∽△ADE。由，得∠BAD=∠DBC；由DE∥BC，得∠EDB=∠DBC；又∠BDE=∠BAD，因此△DBE∽△ADE。8. （江苏省苏州市2007年8分）如图，BC是⊙O的直径，点A在圆上，且AB=AC=4．P为AB上一点，过P作PE⊥AB分别BC、OA于E、F (1)设AP=1，求△OEF的面积． (2)设AP=a (0＜a＜2)，△APF、△OEF的面积分别记为S1、S2。①若S1=S2，求a的值；②若S= S1+S2，是否存在一个实数a，使S＜?若存在，求出一个a的值；若不存在，说明理由．【答案】解：(1)∵BC是⊙O的直径，∴∠BAC=90°。又∵ AB=AC，∴∠B=∠

∵DE∥BC，∴∠EDB=∠DBC。

∵∠DBC所对的是弧，∠EAD所对的是弧，

且，

∴∠DBC=∠EAD。∴∠EDB=∠EAD。

又∠DEB=∠AED，∴△DBE∽△ADE。

【考点】圆周角定理，平行线的性质，等腰三角形的判定，相似三角形的判定和性质。

【分析】（1）由DE∥BC，可得∠ABC=∠E；由∠ADB，∠C都是AB所对的圆周角，得∠ADB=∠C；又∠ABC=∠C，因此∠ADB=∠E。

（2）由∠ABC=∠C得AB=AC；由△ADB∽△AED得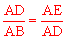；即AD2=AB•AE=AC•AE。

（3）点D运动到弧BC中点时，△DBE∽△ADE。由，得∠BAD=∠DBC；由DE∥BC，得∠EDB=∠DBC；又∠BDE=∠BAD，因此△DBE∽△ADE。

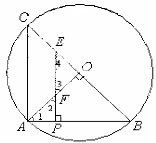
8. （江苏省苏州市2007年8分）如图，BC是⊙O的直径，点A在圆上，且AB=AC=4．P为AB上一

点，过P作PE⊥AB分别BC、OA于E、F

　　　 (1)设AP=1，求△OEF的面积．

　 　 (2)设AP=a (0＜a＜2)，△APF、△OEF的面积分别记为S1、S2。

①若S1=S2，求a的值；

②若S= S1+S2，是否存在一个实数a，使S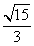＜?若存在，求出一个a的值；若不存在，说明理由．

【答案】解：(1)∵BC是⊙O的直径，∴∠BAC=90°。

　　　　　　　　　　　又∵ AB=AC，∴∠B=∠C=45°。

∵OA⊥BC，∴∠B=∠1=45°。∵PE⊥ AB，∴∠2=∠1=45°。∴∠4=∠3=45°。

则△APF、△OEF与△OAB均为等腰直角三角形。

　　　　　　　　　　　∵AP=l，AB=4，∴AF=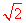，OA=。∴OE=OF=。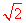

　　　　　　　　　　　∴△OEF的面积为。

　　　　　　(2)①∵PF=AP=a．∴AF=．OE=OF=一。

∴，

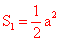∵S1=S2 ，∴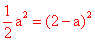

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页