圆形练习题及答案（一）

概要：C、D为顶点的三角形与以B、C、O为顶点的三角形相似？请写出解答过程．【答案】解: (1)。（2）∵∠BOD是△BOC的外角，∠BCO是△ACD的外角， ∴∠BOD＝∠B＋∠BCO，∠BCO＝∠A＋∠D。∴∠BOD＝∠B＋∠A＋∠D。又∵∠BOD和∠A分别是弧BD所对的圆心角和圆周角， ∴∠BOD＝2∠A。又∵∠B＝30°，∠D＝20°，∴2∠A＝∠A＋30°＋20°，即∠A＝50°。∴∠BOD＝2∠A＝100°。（3）∵∠BCO＝∠A＋∠D，∴∠BCO＞∠A，∠BCO＞∠D。∴要使△DAC∽△BOC，只能∠DCA＝∠BCO＝90°。此时∠BOC＝60°，∠BOD＝120°，∴∠DAC＝6

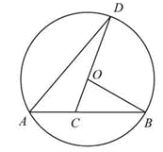
10. （江苏省苏州市2011年8分）如图，已知AB是⊙O的弦，OB＝2，∠B＝30°，C是弦AB上的任意一点（不与点A、B重合），连接CO并延长CO交于⊙O于点D，连接AD．

　　　 (1)弦长AB等于　 ▲　 （结果保留根号）；

　　　 (2)当∠D＝20°时，求∠BOD的度数；

　　　 (3)当AC的长度为多少时，以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似？请写出解

答过程．

【答案】解: (1)。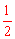

　　　　　　（2）∵∠BOD是△BOC的外角，∠BCO是△ACD的外角，

　　　　　　　　　　 ∴∠BOD＝∠B＋∠BCO，∠BCO＝∠A＋∠D。∴∠BOD＝∠B＋∠A＋∠D。

　　　　　　　　　　　　又∵∠BOD和∠A分别是弧BD所对的圆心角和圆周角， ∴∠BOD＝2∠A。

　　　　　　　　　　　　又∵∠B＝30°，∠D＝20°，∴2∠A＝∠A＋30°＋20°，即∠A＝50°。

　　　　　　　　　　　∴∠BOD＝2∠A＝100°。

　　　　　　　（3）∵∠BCO＝∠A＋∠D，∴∠BCO＞∠A，∠BCO＞∠D。

　　　　　　　　　　　　∴要使△DAC∽△BOC，只能∠DCA＝∠BCO＝90°。

　　　　　　　　　　　　　　此时∠BOC＝60°，∠BOD＝120°，∴∠DAC＝60°。

　　　　　　　　　　　　∴△DAC∽△BOC。

　　　　　　　　　　　∵∠BCO＝90°，即OC⊥AB，∴AC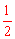＝AB＝。

　　　　　　　　　　　　∴当AC＝时，以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似。

【考点】弦径定理， 直角三角函数， 圆周角定理， 三角形外角定理，相似三角形的判定。

【分析】(1) 由OB＝2，∠B＝30°知。

(2) 由∠BOD是圆心角，它是圆周角A的两倍， 而得求。

(3)要求AC的长度为多少时，△DAC∽△BOC，只能∠DCA＝∠BCO＝90°，据此可求。

11. （2012江苏苏州8分）如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为.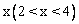

⑴当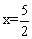 时，求弦PA、PB的长度；

⑵当x为何值时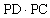，的值最大？最大值是多少？

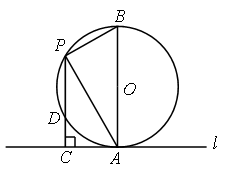
【答案】解：（1）∵⊙O与直线l相切于点A，AB为⊙O的直径，∴AB⊥l。

又∵PC⊥l，∴AB∥PC. ∴∠CPA=∠PAB。

∵AB为⊙O的直径，∴∠APB=90°。

∴∠PCA=∠APB.∴△PCA∽△APB。

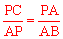∴，即PA2=PC·PD。

∵PC=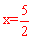

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页