圆形练习题及答案(一)
概要:EDF ,③DE是⊙O的切线,④。其中一定成立的是()A. ①②③ B. ②③④C. ①③④ D. ①②④【答案】D。【考点】角平分线的性质,全等三角形的判定和性质,平角定义,四边形内角和定理,切线的判定,圆周角定理。【分析】①∵CD是∠ACE的平分线,∴∠DCE=∠DCF。∵DF⊥AC,DE⊥BC,∴∠DEC=∠DFC=900。又∵DC=DC,∴△CDE≌△CDF(AAS)。∴CE=CF。∴①正确。②∵根据四边形内角和定理∠ACE+∠EDF+∠DEC+∠DFC=3800和∠DEC=∠DFC=900,∴∠ACE+∠EDF=180°。又∵∠ACB+∠ACE=180°,∴∠ACB=∠EDF。∴②正确。③如图,连接OD、OC,则∠ODC=∠OCD。 ∴∠ODE=∠OCD+∠CDE=∠OCD+900-∠D
圆形练习题及答案(一),http://www.jdxx5.com∵四边形ABCD内接于⊙O,∴∠BAD+∠BCD=180°。
又∵∠BAD=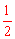 ∠BOD=80°,∴∠BCD=180°-∠BAD=100°。
∠BOD=80°,∴∠BCD=180°-∠BAD=100°。
故选B。
5.(江苏省苏州市2002年3分)如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D。
DF⊥AC,垂足为F,DE⊥BC,垂足为E。
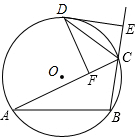 给出下列4个结论:①CE=CF,②∠ACB=∠EDF ,③DE是⊙O的切线,④
给出下列4个结论:①CE=CF,②∠ACB=∠EDF ,③DE是⊙O的切线,④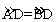 。其中一定成立的是( )
。其中一定成立的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
【答案】D。
【考点】角平分线的性质,全等三角形的判定和性质,平角定义,四边形内角和定理,切线的判定,圆周角定理。
【分析】①∵CD是∠ACE的平分线,∴∠DCE=∠DCF。
∵DF⊥AC,DE⊥BC,∴∠DEC=∠DFC=900。
又∵DC=DC,∴△CDE≌△CDF(AAS)。∴CE=CF。∴①正确。
②∵根据四边形内角和定理∠ACE+∠EDF+∠DEC+∠DFC=3800和∠DEC=∠DFC=900,
 ∴∠ACE+∠EDF=180°。
∴∠ACE+∠EDF=180°。
又∵∠ACB+∠ACE=180°,∴∠ACB=∠EDF。∴②正确。
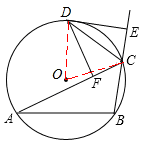
③如图,连接OD、OC,则∠ODC=∠OCD。
∴∠ODE=∠OCD+∠CDE=∠OCD+900-∠DCE
=∠DCA-∠OCF+900-∠DCE=900-∠OCF≠900。
∴DE不是⊙O的切线。∴③错误。
【只有当∠OCF=0,即AC是圆的直径时,DE才是⊙O的切线。同样可证,当圆心O在△ABC内时,∠ODE=900+∠OCF≠900,DE也不是⊙O的切线。】
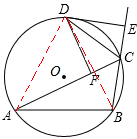 ④如图,连接AD,BD。
④如图,连接AD,BD。
根据圆内接四边形的外角等于内对角得∠DCE=∠DAB,
又∵∠DCE=∠DCF,∠DCA=∠DBA,
∴∠DAB=∠DBA<900。∴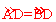 。
。
综上所述,①②④正确。故选D。
6.(江苏省苏州市2003年3分)如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=700,则
∠BOD=( )
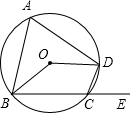
A. 350 B. 700 C. 1100 D. 1400
【答案】D。
【考点】圆内接四边形的性质,圆周角定理。
【分析】根据圆的内接四边形外角等于内对角求出∠A=∠DCE=70°,再根据同弧所对圆心角等于圆周角一半的圆周角定理,可求∠BOD=2∠A=140°。故选D。
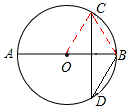
7.(江苏省苏州市2004年3分)如图,AB是⊙的直径,弦CD垂直平分OB,则∠BDC=( )
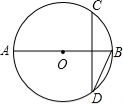
A.15° B.20° C.30° D.45°
【答案】
【考点】圆周角定理,线段垂直平分线的性质,等边三角形的判定和性质。
【分析】连接OC,BC,
∵弦CD垂直平分OB,
∴根据线段垂直平分线上的点到线段两端距离相等的性质,得OC=BC。
又∵OC=OB,∴△OCB是等边三角形。
∴∠COB=60°。
∴根据同弧所对圆周角是圆心角一半的圆周角定理,得∠D=30°。故选C。
8.(江苏省苏州市2008年3分)如图.AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四个结论:
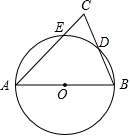
①∠A=45°; ②AC=AB: ③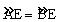 ; ④CE·AB=2BD2.
; ④CE·AB=2BD2.
其中正确结论的序号是( )
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页

- 圆形练习题及答案(一)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
