圆形练习题及答案（一）

概要：AB．若∠ABD=65°，则∠ADC= ▲ ．【答案】25°。【考点】圆周角定理，平行线的性质，直角三角形两锐角的关系。【分析】∵CD∥AB，∴∠ADC=∠BAD。又∵AB是⊙O的直径，∴∠ADB=90°。又∵∠ABD=65°，∴∠ADC=∠BAD=90°－∠ABD=25°。7. （江苏省2009年3分）已知正六边形的边长为1cm，分别以它的三个不相邻的顶点为圆心，1cm长为半径画弧（如图），则所得到的三条弧的长度之和为 ▲ cm（结果保留）．【答案】。【考点】正六边形的性质，扇形弧长公式。【分析】如图，连接AC，则由正六边形的性质知，扇形ABmC中，半径AB=1，圆心角∠BAC=600，∴弧长。由正六边形的对称性，知，所得到的三条弧的长度之和为弧长的6倍，即。8.（江苏省苏州市2010年3分）如图，在4×4的方格纸中(共有16个小方格)，每个小方格都是边长为1的正方形． 、、分别是小正方形的顶点，则扇形的弧长等于 ▲ ．(结果保留根号及)．【答案】。

5. （江苏省苏州市2007年3分）如图，已知扇形的半径为3cm，圆心角为120°，则扇形的面积为­­­­­­­­­­­­­­­­­­­­­­　　 ▲　　 cm2

（结果保留）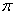

【答案】。

【考点】扇形面积的计算。

【分析】把相应数值代入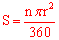求值即可：。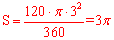

6. （江苏省2009年3分）如图，AB是⊙O的直径，弦CD∥AB．若∠ABD=65°，则∠ADC=　　 ▲　　 ．

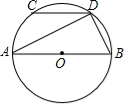
【答案】25°。

【考点】圆周角定理，平行线的性质，直角三角形两锐角的关系。

【分析】∵CD∥AB，∴∠ADC=∠BAD。

又∵AB是⊙O的直径，∴∠ADB=90°。

又∵∠ABD=65°，∴∠ADC=∠BAD=90°－∠ABD=25°。

7. （江苏省2009年3分）已知正六边形的边长为1cm，分别以它的三个不相邻的顶点为圆心，1cm长为半径画弧（如图），则所得到的三条弧的长度之和为　　 ▲　　 cm（结果保留）．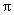

【答案】。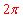

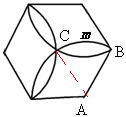【考点】正六边形的性质，扇形弧长公式。

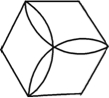
【分析】如图，连接AC，则由正六边形的性质知，扇形ABmC中，半径AB=1，圆心角∠BAC=600，∴弧长。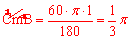

　　　由正六边形的对称性，知，所得到的三条弧的长度之和为弧长的6倍，即。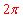

8.（江苏省苏州市2010年3分）如图，在4×4的方格纸中(共有16个小方格)，每个小方格都是边长为1的正方形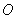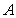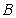． 、、分别是小正方形的顶点，则扇形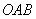的弧长等于　 ▲　 ．(结果保留根号及)．

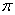【答案】。

【考点】扇形的弧长公式。

【分析】由图形可知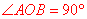，扇形的半径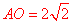

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]  下一页