圆形练习题及答案(二)
概要:中,∵∠ODF=90°,sin∠F=,∴OF=3OD=3R。∵OF+OA=AF,∴3R+R=12,∴R=3。连接BC,则∠ACB=90°。∵∠E=90°,∴BC∥EF。∴AC:AE=AB:AF。∴AC:4=2R:4R,∴AC=2。∴⊙O的半径为3,AC的长为2。【考点】弧、圆周角和圆心角的关系,圆周角定理,平行的判定和性质,切线的判定,锐角三角函数定义,平行线分线段成比例定理。【分析】(1)连接OD,根据圆周角定理,可得∠BOD=∠A,则OD∥AC,从而得出∠ODF=90°,即EF是⊙O的切线。(2)先解直角△AEF,由sin∠F=,得出AF=3AE=12,再在Rt△ODF中,由sin∠F=,得出OF=3OD,设⊙O的半径为R,由AF=12列出关于R的方程,解方程即可求出⊙O的半径。连接BC,证明BC∥EF,根据平行线分线段成比例定理得出AC:AE=AB:AF,即可求出AC的长。4.(2012贵州黔东南12分)如图,⊙O是△ABC的
圆形练习题及答案(二),http://www.jdxx5.com,AE=4,求⊙O的半径和AC的长。
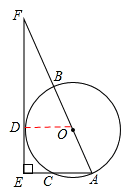 【答案】(1)证明:连接OD,
【答案】(1)证明:连接OD,
∵D是 的中点,∴∠BOD=∠A。
的中点,∴∠BOD=∠A。
∴OD∥AC。
∵EF⊥AC,∴∠E=90°。∴∠ODF=90°。
∴EF是⊙O的切线;
(2)解:在△AEF中,∵∠E=90°,sin∠F=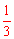 ,AE=4,
,AE=4,
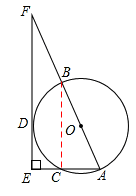 ∴
∴ 。
。
设⊙O的半径为R,则OD=OA=OB=R,AB=2R.
在△ODF中,∵∠ODF=90°,sin∠F=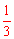 ,∴OF=3OD=3R。
,∴OF=3OD=3R。
∵OF+OA=AF,∴3R+R=12,∴R=3。
连接BC,则∠ACB=90°。
∵∠E=90°,∴BC∥EF。∴AC:AE=AB:AF。
∴AC:4=2R:4R,∴AC=2。
∴⊙O的半径为3,AC的长为2。
【考点】弧、圆周角和圆心角的关系,圆周角定理,平行的判定和性质,切线的判定,锐角三角函数定义,平行线分线段成比例定理。
【分析】(1)连接OD,根据圆周角定理,可得∠BOD=∠A,则OD∥AC,从而得出∠ODF=90°,即EF是⊙O的切线。
(2)先解直角△AEF,由sin∠F=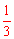 ,得出AF=3AE=12,再在Rt△ODF中,由sin∠F=
,得出AF=3AE=12,再在Rt△ODF中,由sin∠F=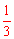 ,得出OF=3OD,设⊙O的半径为R,由AF=12列出关于R的方程,解方程即可求出⊙O的半径。连接BC,证明BC∥EF,根据平行线分线段成比例定理得出AC:AE=AB:AF,即可求出AC的长。
,得出OF=3OD,设⊙O的半径为R,由AF=12列出关于R的方程,解方程即可求出⊙O的半径。连接BC,证明BC∥EF,根据平行线分线段成比例定理得出AC:AE=AB:AF,即可求出AC的长。
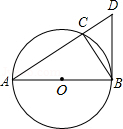
4.(2012贵州黔东南12分)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
(1)求证:△ABC∽△BDC.
(2)若AC=8,BC=6,求△BDC的面积.

5.(2012贵州黔南10分)已知,如图,点C在以AB为直径的⊙O上,点D在AB的的延长线上,∠BCD=∠A。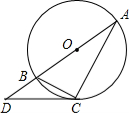
(1)求证:CD是⊙O的切线;
(2)过点C作CE⊥AB于E。若CE=2,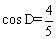 ,求AD的长。
,求AD的长。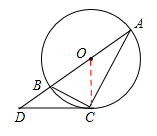
【答案】解:(1)证明:连接CO,
∵AB是⊙O直径,∴∠ACO+∠OCB=90°。
∵AO=CO,∴∠ACO =∠A。
∵∠BCD=∠A,∴∠BCD +∠OCB=90°,即∠OCD=90°。
∴OC⊥CD。
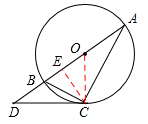 又∵OC是⊙O半径,∴CD为⊙O的切线。[来源:学_科_网]
又∵OC是⊙O半径,∴CD为⊙O的切线。[来源:学_科_网]
(2)∵OC⊥CD于C,∴∠COD +∠D=90°。
∵CE⊥AB于E,∴∠COD +∠OCE=90°。∴∠OCE =∠D。
∴cos∠OCE =cosD。
在△OCE中,∠OEC=90°,∴cos∠OCE =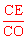 。
。
∵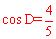
上一页 [1] [2] [3] [4] [5] [6] [7] 下一页

- 圆形练习题及答案(二)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
