圆形练习题及答案(二)
概要:Rt△ACE中,∵OC=AC,OE=AE,∴Rt△OCE≌Rt△ACE(HL)。又∵S扇形OEC=S扇形AEC,∴与弦OC围成的弓形的面积等于与弦AC所围成的弓形面积。同理可得,与弦OC围成的弓形的面积等于与弦BC所围成的弓形面积。∴S阴影=S△AOB=×1×1=(cm2)。故选C。二、填空题1.(2012贵州六盘水4分)已知两圆的半径分别为2和3,两圆的圆心距为4,那么这两圆的位置关系是▲.【答案】相交。【考点】圆与圆的位置关系。【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,∵两圆的半径分别为2和3,两圆的圆心距为4,∴2+3=5,3﹣2=1。∵1<4<5,∴这两圆的位置关系是相交。2.(2012贵州六盘水4分)如图,已知∠OCB=20°,则∠A=▲度.【答案】70°。【考点】等腰三角形的性质,三角形内角和定理,圆周角定理
圆形练习题及答案(二),http://www.jdxx5.comπcm2 C.
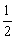 cm2 D.
cm2 D. cm2
cm2
【答案】C。
【考点】等腰直角三角形的判定和性质,圆周角定理,全等三角形的判定和性质。
【分析】如图,过点C作CD⊥OB,CE⊥OA,垂足分别为点D、E。
∵OB=OD,∠AOB=90°,∴△AOB是等腰直角三角形。
∵OA是直径,∴∠ACO=90°。∴△AOC是等腰直角三角形。
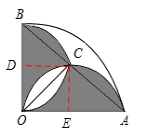
∵CE⊥OA,∴OE=AE=OC=AC。
在Rt△OCE与Rt△ACE中,∵OC=AC,OE=AE,∴Rt△OCE≌Rt△ACE(HL)。
又∵S扇形OEC=S扇形AEC,
∴ 与弦OC围成的弓形的面积等于
与弦OC围成的弓形的面积等于 与弦AC所围成的弓形面积。
与弦AC所围成的弓形面积。
同理可得, 与弦OC围成的弓形的面积等于
与弦OC围成的弓形的面积等于 与弦BC所围成的弓形面积。
与弦BC所围成的弓形面积。
∴S阴影=S△AOB= ×1×1=
×1×1= (cm2)。故选C。
(cm2)。故选C。
二、填空题
1.(2012贵州六盘水4分)已知两圆的半径分别为2和3,两圆的圆心距为4,那么这两圆的位置关系是▲ .
【答案】相交。
【考点】圆与圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,
∵两圆的半径分别为2和3,两圆的圆心距为4,∴2+3=5,3﹣2=1。
∵1<4<5,∴这两圆的位置关系是相交。
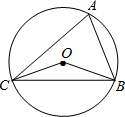
2.(2012贵州六盘水4分)如图,已知∠OCB=20°,则∠A= ▲ 度.
【答案】70°。
【考点】等腰三角形的性质,三角形内角和定理,圆周角定理。
【分析】由OB=OC与∠OCB=20°,根据等边对等角的性质,即可求得∠OBC=20°。
由三角形内角和定理,得∠BOC=180°﹣∠OCB﹣∠OBC=180°﹣20°﹣20°=140°。
由同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半的性质,即可求得∠A=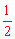 ∠BOC=70°。
∠BOC=70°。
3.(2012贵州六盘水4分)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 ▲ cm.
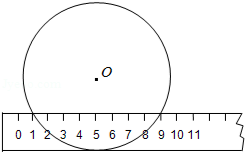
【答案】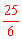 。
。
【考点】垂径定理,勾股定理。
【分析】如图,连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,∴AD=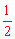 AB=
AB=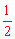 (9﹣1)=4。
(9﹣1)=4。
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=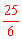
上一页 [1] [2] [3] [4] [5] [6] [7] 下一页

- 圆形练习题及答案(二)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
