圆形练习题及答案（二）

概要：4;BD=BC=。（2）连接OD，∵O是AB的中点，D是BC的中点，∴OD是△ABC的中位线，所以OD⊥AB，故，所以与弦BD组成的弓形的面积等于与弦AD组成的弓形的面积，∴。从而可得出结论。2.（2012贵州安顺12分）如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB=40°，∠APD=65°．（1）求∠B的大小；（2）已知AD=6，求圆心O到BD的距离．【答案】解：（1）∵∠APD=∠C+∠CAB，∠CAB=40°，∠APD=65°，∴∠C=65°﹣40°=25°。∴∠B=∠C=25°。（2）过点O作OE⊥BD于E，则DE=BE，又∵AO=BO，∴OE=AD=×6=3。∴圆心O到BD的距离为3。【考点】圆周角定理，三角形外角性质，垂径定理，三角形中位线定理。【分析】（1）根据圆周定理以及三角形外角求出即可。（2）利用三角形中位线定理得出OE= AD，即可得出答案。3.（20

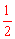∴ =AB•AC﹣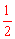AB•OD=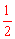×2×2﹣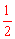×2×1=2﹣1=1。

【考点】切线的性质，勾股定理，圆周角定理，扇形面积的计算。

【分析】（1）连接AD，

∵AC是⊙O的切线，∴AB⊥AC。

∵∠C=45°，∴AB=AC=2。∴。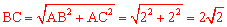

∵AB是⊙O的直径，∴∠ADB=90°。∴D是BC的中点。∴BD=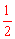BC=。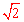

（2）连接OD，∵O是AB的中点，D是BC的中点，∴OD是△ABC的中位线，所以OD⊥AB，故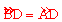，所以与弦BD组成的弓形的面积等于与弦AD组成的弓形的面积，∴。从而可得出结论。　

2.（2012贵州安顺12分）如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB=40°，∠APD=65°．

（1）求∠B的大小；

（2）已知AD=6，求圆心O到BD的距离．

【答案】解：（1）∵∠APD=∠C+∠CAB，∠CAB=40°，∠APD=65°，

∴∠C=65°﹣40°=25°。

∴∠B=∠C=25°。

（2）过点O作OE⊥BD于E，则DE=BE，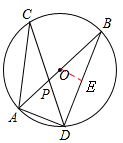

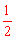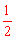又∵AO=BO，∴OE=AD=×6=3。

∴圆心O到BD的距离为3。

【考点】圆周角定理，三角形外角性质，垂径定理，三角形中位线定理。

【分析】（1）根据圆周定理以及三角形外角求出即可。

（2）利用三角形中位线定理得出OE=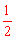 AD，即可得出答案。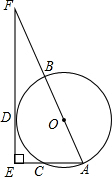

3.（2012贵州毕节14分）如图，AB是⊙O的直径，AC为弦，D是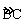的中点，过点D作EF⊥AC的延长线于E，交AB的延长线于E，交AB的延长线于F。

（1）求证：EF是⊙O的切线；

（2）若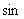∠F=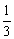

上一页  [1] [2] [3] [4] [5] [6] [7]  下一页