圆形练习题及答案(四)
[10-09 23:31:05] 来源:http://www.jdxx5.com 初三数学试题 阅读:92149次
概要:,∴n=120,即圆锥侧面展开图的圆心角是120°.∴∠APB=60°.在圆锥侧面展开图中,AP=9,PC=4.5,可知∠ACP=90°.∴.故从A点到C点在圆锥的侧面上的最短距离为.点评:本题需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.26.分析:利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径和母线长的关系,进而利用勾股定理可求得各个圆锥的高,比较即可.解:设扇形做成圆锥的底面半径为,由题意知,扇形的圆心角为240°,则它的弧长=,解得,由勾股定理得,.设扇形做成圆锥的底面半径为,由题意知,扇形的圆心角为120°,则它的弧长=,解得,由勾股定理得,所以>.上一页 [1] [2] [3] [4] [5] [6] [7] [8]
圆形练习题及答案(四),http://www.jdxx5.com,
∴n=120,即圆锥侧面展开图的圆心角是120°.
∴∠APB=60°.
在圆锥侧面展开图中,AP=9,PC=4.5,可知∠ACP=90°.
∴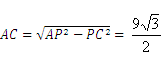 .
.
故从A点到C点在圆锥的侧面上的最短距离为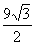 .
.
点评:本题需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.
26.分析:利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径和母线长的关系,进而利用勾股定理可求得各个圆锥的高,比较即可.
解:设扇形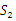 做成圆锥的底面半径为
做成圆锥的底面半径为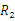 ,
,
由题意知,扇形 的圆心角为240°,
的圆心角为240°,
则它的弧长=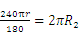 ,解得
,解得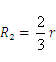 ,
,
由勾股定理得, .
.
设扇形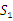 做成圆锥的底面半径为
做成圆锥的底面半径为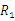 ,
,
由题意知,扇形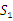 的圆心角为120°,
的圆心角为120°,
则它的弧长=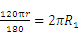 ,解得
,解得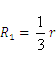 ,
,
由勾股定理得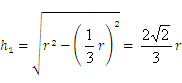 ,所以
,所以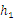 >
>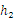 .
.
上一页 [1] [2] [3] [4] [5] [6] [7] [8]
标签:初三数学试题,九年级数学试题,初中数学学习方法,初中学习 - 初三学习 - 初三数学 - 初三数学试题

- 圆形练习题及答案(四)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
最新《初三数学试题》
热门《初三数学试题》
