圆形练习题及答案(四)
概要:AB是⊙O的直径,∴ BD⊥AD.又∵ CF⊥AD,∴ BD∥CF.∴ ∠BDC=∠C.又∵ ∠BDC=∠BOC,∴ ∠C=∠BOC.∵ AB⊥CD,∴ ∠C=30°,∴ ∠ADC=60°.点拨:直径所对的圆周角等于90°,在同一个圆中,同一条弧所对的圆心角等于圆周角的2倍.20. 解:连接AE,则AE⊥BC.由于E是BC的中点,则AB=AC,∠BAE=∠CAE,则BE=DE=EC,S弓形BE=S弓形DE,∴ S阴影=S△DCE.由于∠BED=120°,则△ABC与△DEC都是等边三角形,∴ S△DCE=×2×=.21.分析:(1)欲求∠DEB,已知一圆心角,可利用圆周角与圆心角的关系求解.(2)利用垂径定理可以得到,从而的长可求.解:(1)连接,∵ ,∴ ,弧AD=弧BD,∴ 又,∴ .(2)∵,&th
解析:扇形的弧长l=
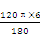 =4π(cm),所以圆锥的底面半径为4π÷2π=2(cm),所以这个圆锥形纸帽的高为
=4π(cm),所以圆锥的底面半径为4π÷2π=2(cm),所以这个圆锥形纸帽的高为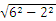 = 4
= 4 (cm).
www.jdxx5.com
(cm).
www.jdxx5.com
三、解答题
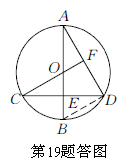 19.分析:连接BD,易证∠BDC=∠C,∠BOC=2∠BDC=2∠C,∴ ∠C=
19.分析:连接BD,易证∠BDC=∠C,∠BOC=2∠BDC=2∠C,∴ ∠C=
30°, 从而∠ADC=60°.
解:连接BD.∵ AB是⊙O的直径,∴ BD⊥AD.
又∵ CF⊥AD,∴ BD∥CF.∴ ∠BDC=∠C.
又∵ ∠BDC= ∠BOC,∴ ∠C=
∠BOC,∴ ∠C= ∠BOC.
∠BOC.
∵ AB⊥CD,∴ ∠C=30°,∴ ∠ADC=60°.
点拨:直径所对的圆周角等于90°,在同一个圆中,同一条弧所对
的圆心角等于圆周角的2倍.
20. 解:连接AE,则AE⊥BC.由于E是BC的中点,则AB=AC,∠BAE=∠CAE,则BE=DE=EC,S弓形BE=S弓形DE,∴ S阴影=S△DCE.由于∠BED=120°,则△ABC与△DEC都是等边三角形,∴ S△DCE= ×2×
×2×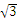 =
=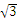 .
.
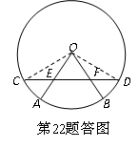
21.分析:(1)欲求∠DEB,已知一圆心角,可利用圆周角与圆心角的关系求解.
(2)利用垂径定理可以得到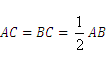 ,从而
,从而 的长可求.
的长可求.
解:(1)连接 ,∵
,∵ 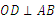 ,∴
,∴ 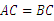 ,弧AD=弧BD,
,弧AD=弧BD,
∴ 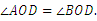 又
又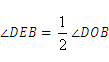 ,
,
 ∴
∴ 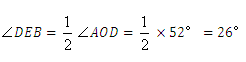 .
.
(2)∵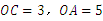 ,∴
,∴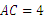 .
.
又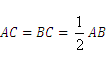 ,∴
,∴ 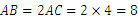
上一页 [1] [2] [3] [4] [5] [6] [7] [8] 下一页

- 圆形练习题及答案(四)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
