圆形练习题及答案(四)
概要:.22.分析:要证明△OEF是等腰三角形,可以转化为证明,通过证明△OCE≌△ODF即可得出.证明:如图,连接OC、OD,则,∴ ∠OCD=∠ODC.在△OCE和△ODF中,∴△OCE≌△ODF(SAS),∴,从而△OEF是等腰三角形.23.分析:由圆周角定理,得,;已知,联立三式可得.解:.理由如下:∵ ,,又,∴ .24.解:(1)已知桥拱的跨度AB=16米,拱高CD=4米,∴ AD=8米.利用勾股定理可得,解得OA=10(米).故桥拱的半径为10米.(2)当河水上涨到EF位置时,因为∥,所以,∴ (米),连接OE,则OE=10米,(米).又,所以(米),即水面涨高了2米.25.分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.解:由题意可知圆锥的底面周长是,则上一页 [1] [2] [3] [4] [5] [6] [7] [8] 下一页
圆形练习题及答案(四),http://www.jdxx5.com.
22.分析:要证明△OEF是等腰三角形,可以转化为证明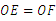 ,通过证明△OCE≌△ODF即可得出.
,通过证明△OCE≌△ODF即可得出.
证明:如图,连接OC、OD,则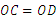 ,
,
∴ ∠OCD=∠ODC.
在△OCE和△ODF中,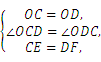
∴△OCE≌△ODF(SAS),
∴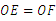 ,从而△OEF是等腰三角形.
,从而△OEF是等腰三角形.
23.分析:由圆周角定理,得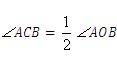 ,
,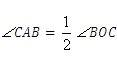 ;已知
;已知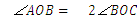 ,联立三式可得.
,联立三式可得.
解: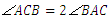 .理由如下:
.理由如下:
∵ 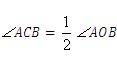 ,
,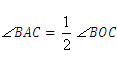 ,
,
又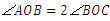 ,∴
,∴ 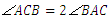 .
.
24.解:(1)已知桥拱的跨度AB=16米,拱高CD=4米,
∴ AD=8米.利用勾股定理可得
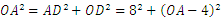 ,解得OA=10(米).
,解得OA=10(米).
故桥拱的半径为10米.
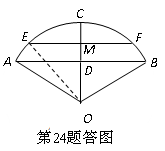 (2)当河水上涨到EF位置时,因为
(2)当河水上涨到EF位置时,因为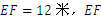 ∥
∥ ,所以
,所以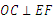 ,
,
∴  (米),
(米),
连接OE,则OE=10米,
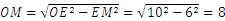 (米).
(米).
又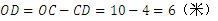 ,
,
所以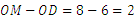 (米),即水面涨高了2米.
(米),即水面涨高了2米.
25.分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.
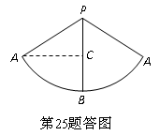 解:由题意可知圆锥的底面周长是
解:由题意可知圆锥的底面周长是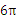 ,则
,则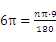
上一页 [1] [2] [3] [4] [5] [6] [7] [8] 下一页

- 圆形练习题及答案(四)
- › 圆形练习题及答案汇总
- › 圆形练习题及答案(十)
- › 圆形练习题及答案(一)
- › 圆形练习题及答案(二)
- › 圆形练习题及答案(三)
- › 圆形练习题及答案(四)
- › 圆形练习题及答案(五)
- › 圆形练习题及答案(六)
- › 圆形练习题及答案(七)
- › 圆形练习题及答案(八)
- › 圆形练习题及答案(九)
