高二上册数学(文科)寒假作业及答案
概要:there4;有5. ,令得,故切点为,代入直线方程,得,所以。6. 2 -2 7.解:f′(x)=ex.①(1)当a=时,若f′(x)=0,则4x2-8x+3=0,解得x1=,x2=.结合①可知所以,x1=是极小值点,x2=是极大值点.(2)若f(x)为R上的单调函数,则f′(x)在R上不变号,结合①与条件a>0,知ax2-2ax+1≥0在R上恒成立,因此Δ=4a2-4a=4a(a-1)≤0,由此并结合a>0,知08.解:(1)因为x=5时,y=11,所以+10=11,a=2.x k b 1 .c o m(2)由(1)可知,该商品每日的销售量y=+10(x-6)2. 所以商场每日销售该商品所获得的利润f(x)=(x-3)=2+10(x-3)(x-6)2,3从而f′(x)=10=30(x-4)(x-6).于是,当x变化时,f′(x),f(x)的变化情况如下表:由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.所以,当x=4时,函数f(x)取得最大值,且最大值等于42.答:当销售价格为4元/千克时,商场每日销售
高二上册数学(文科)寒假作业及答案,http://www.jdxx5.com作业(18)
1. C 令f′(x)=2x-2-=>0,又∵f(x)的定义域为{x|x>0},
∴(x-2)(x+1)>0(x>0),解得x>2
2. A y′=ex,故所求切线斜率k=ex|x=0=e0=1.
3. C因为y′=3x2,所以k=y′|x=1=3,所以过点P(1,12)的切线方程为
y-12=3(x-1),即y=3x+9,所以与y轴交点的纵坐标为9.
4. A 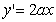 ,于是切线的斜率
,于是切线的斜率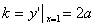 ,∴有
,∴有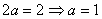
5. 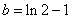
 ,令
,令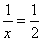 得
得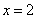 ,故切点为
,故切点为 ,代入直线方程,得
,代入直线方程,得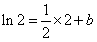 ,所以
,所以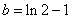 。
。
6. 2 -2 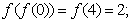
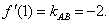
7.解:f′(x)=ex.①
(1)当a=时,若f′(x)=0,则4x2-8x+3=0,解得x1=,x2=.结合①可知
所以,x1=是极小值点,x2=是极大值点.
(2)若f(x)为R上的单调函数,则f′(x)在R上不变号,结合①与条件a>0,知ax2-2ax+1≥0在R上恒成立,因此Δ=4a2-4a=4a(a-1)≤0,由此并结合a>0,知0
8.解:(1)因为x=5时,y=11,所以+10=11,a=2.x k b 1 .c o m
(2)由(1)可知,该商品每日的销售量
y=+10(x-6)2. 所以商场每日销售该商品所获得的利润
f(x)=(x-3)=2+10(x-3)(x-6)2,3
从而f′(
于是,当x变化时,f′(x),f(x)的变化情况如下表:
由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以,当x=4时,函数f(x)取得最大值,且最大值等于42.
答:当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大. x)=10=30(x-4)(x-6).
x)=10=30(x-4)(x-6).
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21]

