高一数学函数奇偶性复习要点

概要：=-f(x)与f(-x)=f(x)都不能成立，那么函数f(x)既不是奇函数又不是偶函数，称为非奇非偶函数。说明：①奇、偶性是函数的整体性质，对整个定义域而言②奇、偶函数的定义域一定关于原点对称，如果一个函数的定义域不关于原点对称，则这个函数一定不是奇（或偶）函数。（分析：判断函数的奇偶性，首先是检验其定义域是否关于原点对称，然后再严格按照奇、偶性的定义经过化简、整理、再与f(x)比较得出结论）③判断或证明函数是否具有奇偶性的根据是定义2．奇偶函数图像的特征：定理 奇函数的图像关于原点成中心对称图表，偶函数的图象关于y轴或轴对称图形。f(x)为奇函数《＝＝》f(x)的图像关于原点对称点（x,y）→（-x,-y）奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。偶函数 在某一区间上单调递增，则在它的对称区间上单调递减。3.奇偶函数运算(1) . 两个偶函数相加所得的和为偶函数。(2) . 两个奇函数相加所得的和为奇函数。(3) . 一个偶函数与一个奇函数相加所得的和为非奇函数与非偶函数。(4) . 两个偶函数相乘所得的积为偶函数。(5) . 两个奇函数相乘所得的积为偶函数。(6) . 一个偶函数与一个奇函数相乘所得的积为奇函数.

　　1．定义

　　一般地，对于函数f(x)

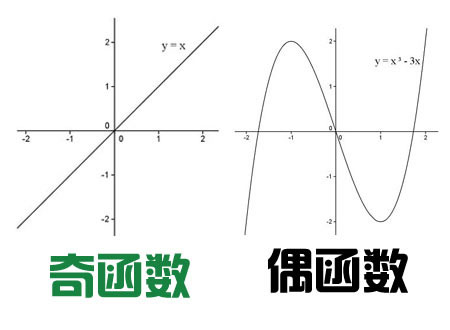
　　（1）如果对于函数定义域内的任意一个x，都有f(-x)=－f(x)，那么函数f(x)就叫做奇函数。

　　（2）如果对于函数定义域内的任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。

　　（3）如果对于函数定义域内的任意一个x，f(-x)=-f(x)与f(-x)=f(x)同时成立，那么函数f(x)既是奇函数又是偶函数，称为既奇又偶函数。

　　（4）如果对于函数定义域内的任意一个x，f(-x)=-f(x)与f(-x)=f(x)都不能成立，那么函数f(x)既不是奇函数又不是偶函数，称为非奇非偶函数。

　　说明：①奇、偶性是函数的整体性质，对整个定义域而言

　　②奇、偶函数的定义域一定关于原点对称，如果一个函数的定义域不关于原点对称，则这个函数一定不是奇（或偶）函数。

　　（分析：判断函数的奇偶性，首先是检验其定义域是否关于原点对称，然后再严格按照奇、偶性的定义经过化简、整理、再与f(x)比较得出结论）

　　③判断或证明函数是否具有奇偶性的根据是定义

　　2．奇偶函数图像的特征：

　　定理 奇函数的图像关于原点成中心对称图表，偶函数的图象关于y轴或轴对称图形。

　　f(x)为奇函数《＝＝》f(x)的图像关于原点对称

　　点（x,y）→（-x,-y）

　　奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。

　　偶函数 在某一区间上单调递增，则在它的对称区间上单调递减。

　　3.奇偶函数运算

　　(1) . 两个偶函数相加所得的和为偶函数。

　　(2) . 两个奇函数相加所得的和为奇函数。

　　(3) . 一个偶函数与一个奇函数相加所得的和为非奇函数与非偶函数。

　　(4) . 两个偶函数相乘所得的积为偶函数。

　　(5) . 两个奇函数相乘所得的积为偶函数。

　　(6) . 一个偶函数与一个奇函数相乘所得的积为奇函数.