2017年中考数学压轴题精选二

概要：于M、N点 ，且MA、NC分别与圆相切于点A和点C．（1）求抛物线的解析式；（2）抛物线的对称轴交x轴于E点 ，连结DE ，并延长DE交圆O于F，求EF的长．（3）过点B作圆O的切线交DC的延长线于点P，判断点P是否在抛物线上，说明理由．解：（1） ∵圆心O在坐标原点，圆O的半径为1，∴点A、B、C、D的坐标分别为A( -1,0)、B（0，-1）、C（1，0）、D（0,1）∵抛物线与直线y=x交于点M、N，且MA、NC分别与圆O相切于点A和点C，∴M（-1，-1），N(1,1)． ∵点D、M、N在抛物线上，将D（0,1）、M(-1,-1)、N(1,1) 的坐标代入，∴抛物线的解析式为： ．---4分（2）∵ ∴抛物线的对称轴为x=0.5，． 6分（3）点P在抛物线上．9分设过D、C点的直线为：y=kx+b，将点C（1,0）D(0,1) 的坐标代入y=kx+b，得：k=-1,b=1，直线DC为y=-x+1： ．---10分过点B作圆O的切线BP与x轴平行，P点的纵坐标为y=-1 ，将y=-1代入y=-x+1，得：x=2．P点的坐标为(2,-1)，当x=2时， ，所以， 点在抛物线 ．-12分

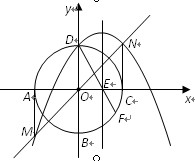
　　如图，在平面直角坐标xoy中，半径为1的圆的圆心o在坐标原点，且与两坐标轴分别交于A、B、C、D四点．抛物线与y 轴交于D点 ，与直线y=x交于M、N点 ，且MA、NC分别与圆相切于点A和点C．

　　（1）求抛物线的解析式；

　　（2）抛物线的对称轴交x轴于E点 ，连结DE ，并延长DE交圆O于F，求EF的长．

　　（3）过点B作圆O的切线交DC的延长线于点P，判断点P是否在抛物线上，说明理由．

　　解：（1） ∵圆心O在坐标原点，圆O的半径为1，

　　∴点A、B、C、D的坐标分别为A( -1,0)、B（0，-1）、C（1，0）、D（0,1）

　　∵抛物线与直线y=x交于点M、N，且MA、NC分别与圆O相切于点A和点C，

　　∴M（-1，-1），N(1,1)． ∵点D、M、N在抛物线上，将D（0,1）、M(-1,-1)、N(1,1) 的坐标代入

　　，

　　∴抛物线的解析式为： ．-----------------------4分

　　（2）∵ 　　

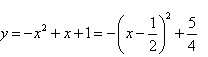
　　∴抛物线的对称轴为x=0.5，

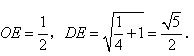　　． 6分

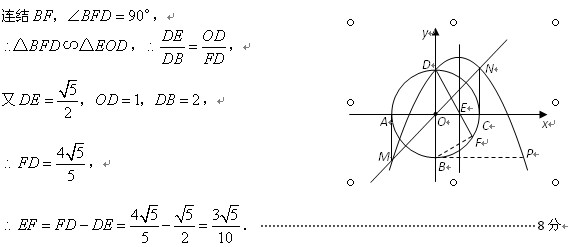
（3）点P在抛物线上．------------------------9分

　　设过D、C点的直线为：y=kx+b，

　　将点C（1,0）D(0,1) 的坐标代入y=kx+b，得：k=-1,b=1，

　　直线DC为y=-x+1： ．-----------------------10分

　　过点B作圆O的切线BP与x轴平行，P点的纵坐标为y=-1 ，

　　将y=-1代入y=-x+1，得：x=2．

　　P点的坐标为(2,-1)，当x=2时， ，

　　所以， 点在抛物线 ．-----------------------------12分